Topic 1

Question 1

What does the taylor series do?

Answer 1

Also known as the power series, the Taylor series form a polynomial with exponential terms that have unique coefficients. Increasing the number of terms i.e. adding exponential values with increasingly larger exponents results in more a accurate approximation for more of the function, however, the taylor series becomes more complex.

The value of the exponent tells us what derivative it affects. For example, x³ influences the third derivate.

It is also important to note that the derivative value of the original function at the chosen point will give the value the Taylor series equivalent term should be equal to.

Question 2

Why are the individual terms in a taylor series divided by the factorial of the x exponent value?

Answer 2

This is done to remove the cascading effect when derivatives are taken.

e.g. the coefficient of x⁵ becomes 5*4*3*2*1 if the 5th derivative is taken.

Question 3

What is the Maclaurin series?

Answer 3

The Maclaurin series is the Taylor series when x₀ = 0

Question 4

What is L’Hopital’s rule ?

Answer 4

Question 5

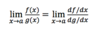
Determine the limit using power series

Answer 5

Question 6

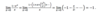
How can L’Hopital’s rule be proven using Taylor Series?

Answer 6

Question 7

Is sine odd or even, and what does that mean?

Answer 7

It is odd and it means that sin (–θ) = –sin θ