Topic 5 Flashcards
(32 cards)
What is the confidence interval estimate?
- a range of numbers, called the interval, constructed around the point estimate (value of a single sample statistic, such as sample mean or sample proportion)
In what way is the confidence interval constructed?
- in such a way that the probability that the population parameter is located somewhere within the interval is known
To compute?


The choice of the confidence interval for the mean depends on what?
- whether sigma population standard deviation (σ) is known or unknown
- whether X is normally distributed or n is large
What assumptions should be made and which confidence interval should be chosen?
n > 30
sigma population standard deviation (σ) is known

What assumptions should be made and which confidence interval should be chosen?
n > 30
sigma population standard deviation (σ) is unknown

What assumptions should be made and which confidence interval should be chosen?
n < 30
sigma population standard deviation (σ) is known

What assumptions should be made and which confidence interval should be chosen?
n < 30
sigma population standard deviation (σ) is unknown

To compute?
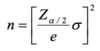
- the sample size required to estimate X bar, for a certain level of confidence
- e is the desired level margin of error
- α is the desired significance level
- σ is the population standard deviation
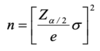
To compute?
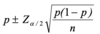
- the confidence interval limit for the proportion
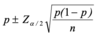
To compute?

- the sample size required to estimate the proportion, p, for a certain level of confidence

The lifetime of particular product is approximately normally distributed with a standard deviation of 400 hrs.
The mean lifetime of a random sample of n = 32 is 4,200 hrs.
Find the 95% confidence interval for estimating the true mean lifetime of the product.
Example: X~N (σ Known)

A large shipment of light bulbs is known to have a normally distributed operating life.
A random sample of 9 bulbs has a mean operating life of 300 hours, and a standard deviation of 45 hours.
Find the 90% confidence interval for the true mean operating life of the entire shipment.
Example: X~N (σ unknown)

For a random sample of 64 buses, Urban Transport Authority knows that the average number of passengers per kilometre is 12.
From earlier studies, it is known that the population standard deviation is 1.6 passengers per kilometre.
Find 95% confidence interval for the average number of passengers per kilometre.
Example: X~? (n is large, σ Known)

A survey of 40 Australian companies indicated that the average annual income of company chief executives was $120 thousand dollars.
Assuming that the population standard deviation is $7.5 (thousand dollars) and the annual incomes are normally distributed:
What is the minimum sample size so you be at least 95% sure that the sample mean would be within $2500 of the true mean?
Sample Size Determination-Mean

A factory produces a component used in manufacturing computers. Each component is tested prior to shipment to determine whether it is defective.
In a random sample of 400 units, 60 were found to be defective.
Estimate, with 99% confidence, the true proportion of defective components produced by the factory. Interpret the results.
Interval Estimation- Proportion

Suppose in the above problem, we want to estimate the proportion of defective components to within 0.03, with 95% confidence.
Find the minimum units should be tested in order to estimate the true proportion.
Sample Size Determination-Proportion



Suppose for the problem outlined in question 1, a random sample of only 16 bags of potato chips were obtained and the average weight was 198 grams and the sample standard deviation of the weights was 3.6 grams.
What would you use as a 95% confidence interval for the true mean weight of the potato chips? State any necessary assumptions for the procedure.


Suppose that the quality control engineer for the manufacture of the potato chip bags in question 1 wanted to find the number of sample potato chip bags to select so that he could be at least 95 per cent sure that the sample mean would be within 0.5 of a gram of the true mean.
What is the minimum sample size that should be taken? Show your work.




Make it 80 per cent.
























