Topic 4 Flashcards
(33 cards)
What is the sampling distribution of a statistic?
- considered as a random variable, when derived from a random sample of size n
- it may also be considered as the distribution of the statistic for all possible samples from the same population of a given size
The mean of the sampling distribution of X bar is the same as what?
- the same as the mean of the random variable that is sampled
The variance of the sampling distribution of X bar is the what?
- the variance of the sampled random variable, divided by the sample size, n
What does the sampling distribution depend on?
- underlying distribution of the parent population
- statistic being considered
- sampling procedure employed
- sample size used
If X is exactly normally distributed then X bar has what?
- it has an exactly normal distribution, no matter what the sample size is
- i.e., if X~N(μ,σ2), then:
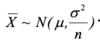
Regardless of the distribution of the sampled random variable, if the sample size is sufficiently large, X bar has what?
- it has an approximately normal distribution
What happens if the sample size exceeds 30?
- then it is large enough for the result of the Central Limit Theorem to be applied
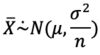
The sampling distribution of the proportion, p, is an application of what?
- the Central Limit Theorem
What is the parental population, X?
(sampling distribution of the sample proportion, p)
- a categorical variable with only two possible outcomes.
- also referred to as Yes/No variables
What is the mean and the variance of the proportion of X?
- π (mean)
- π (1 - π) (variance)
Is the X variable normal?
- the X variable is definitely not normal but, if the sample size is large enough, p, is approximately normally distributed
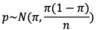
What do we use to evaluate the sampling distribution of the proportion, p?
- we use Z, the standard normal distribution:
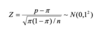
What are the three steps to obtain probabilities for X bar?
- convert value of X bar using the transformation formula:
- draw a diagram and shade the appropriate area under the curve
- read the appropriate value from Table E2
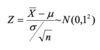
What are the three steps to obtain probabilities for p?
- convert value of p, using the transformation formula:
- draw a diagram and shade the appropriate area under the curve
- read the appropriate value from Table E2
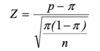
A random sample of 36 is drawn from a normal population with mean equal to 50 and standard deviation 12.
(a) Give the mean and the standard deviation of the sampling distribution of X bar.
(b) Find the value of:
i. P(X bar > 45.5)
ii. P(X bar < 54)
iii. P(X bar > 58)
(c) Find P(X bar > X bar0) = 0.60

For a large population of normally distributed account balances, the mean balance is µ = $150 with standard deviation σ = $35.
(a) What is the probability that one randomly sampled account has a balance that exceeds $160?
(b) What is the probability that the mean random sample of n = 40 accounts will exceed $160?





































