Time value of money - an introduction to financial mathematics Flashcards
(25 cards)
describe the time value of money, and why a dollar today is worth more than a dollar tomorrow
If we receive $1 today we can invest it, earn interest and end up with more than $1 at any time in the future.
how to calculate future value or present value of a single cash flow?
using simple or compound interest calculations
simple interest calculation
compound interest calculation
Simple interest
Future Value = Principal + interest
= PV (1 + rsn)
Compound interest
Future Value = PV (1 + r)n
Future Value of Multiple Cash Flows

–The first deposit ($100) will have been in the bank for exactly two years;
–The second deposit ($200) will have been in the bank for exactly one year; and,
–The third deposit ($500) will be deposited in the bank immediately before the time at which we wish calculate the total value of the deposits.

A finite number of cash flows that are equal in value and are evenly spaced are called
annuities
what are the 3 types of annuities
–Ordinary Annuities;
–Annuities Due; and,
Deferred Annuities.
what is an ordinary annuity?
cash flow occurs at the end of each period

how to calculate future value of an annuity comprising n cash flows of $F immediately following the last cash flow?
compound each cash flow individually or
use the future cash flow of an ordinary annuity formula
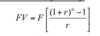


To calculate the present value of an ordinary annuity comprising n cash flows of $F, we use the following equation
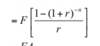
To calculate the present value of an annuity due comprising n cash flows of $F, we use the following equation:
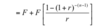
To calculate the present value of a deferred annuity that commences in m periods and comprises n cash flows of $F
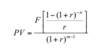
3 types of perpetuities
–Ordinary Perpetuities;
–Perpetuities Due; and,
–Deferred Perpetuities.
The present value of an ordinary perpetuity comprising individual cash flows of $F is calculated as:



present value of an annuity due comprising individual cash flows of $F
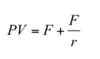
The present value of a deferred perpetuity commencing in m periods and comprising individual cash flows of $F is calculated
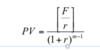
Interest Rates for Time Value of Money Calculations
what is an annual nominal interest rate?
An interest rate where interest is charged more frequently than the time period specified in the interest rate. i.e several compunding periods per annum For example, 12% p.a. compounded monthly is an example of a nominal interest rate

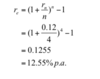

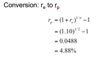


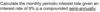
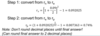
Convert from annual nominal interest rate to an annual effective interest rate
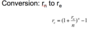
conversion from annual effective interest rate (aka compounded annually) to periodic rate



