Diversification - defining risk and understanding its relationship with return Flashcards
What is a Random Variable?
is one that can take on **any number of different values. ** Each value has an associated probability of occurring. e.g. return of a share
uncertainty associated with the outcome of a random variable is described by
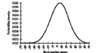
a probability distribution, which illustrates the relative likelihood of each possible outcome occurring. The most commonly used distribution is the normal distribution,
what is used to describe a distribution?
- Mean
- variance
- skewness
- kurtosis
For a normal distribution, the mean is
mean = mode= median
E(x) also is the most likely return on the asset
what does variance measure?
how closely or widely individual values are spread around the mean value. (expected value)
A small variance means that the data doesn’t vary a lot from the mean. A large variance means that the data is more spread out. The standard deviation, s, is simply the square root of the variance.
Kurtosis:
A measure of the “tallness” or “flatness” of the distribution. By definition, the normal distribution has zero excess kurtosis

Suppose the return on the stock market is normally distributed with mean 10% and standard deviation 20%

This distribution demonstrates that it is extremely likely that the return on the market will be between –30% and +50% over the next year. Moreover, there is high probability that the return will be between –10% and +30%
How Do We Calculate the Expected Value of a Random Variable?


How Do We Measure the Risk of a Random Variable?

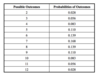
Given E(r)= 7
find standard deviation of the value we expect to roll on the two dice

What Attitude Do Investors Have Towards Risk?
two key assumptions regarding investor preferences:
- Investors prefer more wealth to less; and,
- Investors are risk averse (i.e. they prefer less risk).
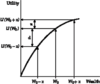
describe the standard utility function
utility function is upward sloping indicates
- that the investor prefers more to less, no matter how wealthy they might become.
- utility function increases at a decreasing rate indicates that the investor is risk averse

For example, suppose that an investor is faced with a gamble whereby they bet $100 on the toss of a coin. If it’s heads they win $200, if it’s tails they get nothing. The gamble creates a 50/50 chance of increasing or decreasing their wealth by $100, so their expected wealth is unchanged. This sort of a gamble is known as a fair bet. However, if the investor is risk averse, they will actually pay to avoid being subjected to this risk.
Proposal: Outcome: +x, -x Probability: 50, 50)
The investor would be pleased if the outcome turns out to be +x, which is illustrated by the increase in utility on the graph (u). However, the investor would be extremely displeased if the outcome turns out to be –x. The decrease in the utility (d) when the outcome is –x is far greater than the increase in the utility when the outcome is +x. This discussion illustrates that in general a risk averse individual will never take a fair bet.
risk averse investors
shy away from risk, therefore, an increase in return on their investment is required to compensate for taking the greater risk
In the presence of risk and uncertainty investors will demand
a risk premium.

If the investor were risk averse, they would never invest in Asset B as it has a higher level of risk than Asset A but the same return.
why do people return in bonds?
as prices of shares can vary considerably over time, return on shares are more volatile and uncertain i.e. share prices and dividends are highly variable
but they do bring greater return
how do bond returns vary over time?
one reason is due to the change in bond prices in response to changes in market interest rates
what is the risk premium
the additional return expected for taking on additional risk


