Arbitrage - options contracts part b Flashcards
The option holder (long position) will only decide to exercise the option
when it benefits them
•Given this, the gain (payoff) the holder makes from the option can be expressed as follows:
–Call Option: payoff(long) = max (ST-X,0); and,
Put Option: payoff(long) = max(X-ST,0)
option holder (long position) will only decide to exercise the option when it benefits them
The payoff for the writer of the option (short position) is exactly the opposite of the payoff for the holder
Call Option: payoff(short) = min(-[ST-X],0) = min(X-ST,0).
Put Option: payoff(short) = min(-[X-ST],0) = min(ST-X,0)
payoff from a long and short position in an European call option

payoff from a long and short position in a European put option

Given the holder of the option will only exercise the option if it benefits them (i.e. their minimum payoff is 0) and the payoff for the writer is the exact opposite of the holder’s payoff (i.e. their maximum payoff is 0), why would anyone want to be the writer of an option?
People write options (i.e. take the short position) in light of the following 2 factors:
- They have the opposite expectation about future price movements as the holder, therefore believing option exercise is unlikely; and,
- In order to write the option, they receive a premium from the holder:
•Call Option: We denote the call option premium as c; and,
•Put Option: We denote the put option premium as p.
the profit for a party to an option is not only the function of the option payoff, but also of the premium
what does this mean?
The holder of the option must also take into account the fact that they have had an additional outflow, namely the option premium; and,
The writer of the option must also take into account the fact that they have had an additional inflow, namely the option premium
what do profit diagrams show?
profit for the option holder is the exact opposite of the profit for the option writer
profit from a long position in a European call option

profit from a short position in a European call option

profit from a long position in a European PUT option

profit from a short position in a European PUT option

Suppose that on March 20, you purchased one contract (for 100 shares) of September $10 BHP call options. At that time, the price of a BHP share was $10.50 and the price of the call options on the Australian Stock Exchange (ASX) was $1.28. That is, at the time of entering the contract, you paid 100 * $1.28 = $128 for the right to purchase 100 BHP shares for $10 each at any time before the contract matures.
It is now September 20, which is the maturity date for September options, and the BHP stock price is $12. Will you exercise the option and, regardless, what is the payoff and profit from the option contract?
In this case, you will want to exercise the option: you pay $10 * 100 = $1,000 and receive 100 BHP shares which are worth $1,200 in total. Hence, the payoff from the option contract is $200 and the profit (net of the initial cost) is $72 ($200-$128)
Suppose that on March 20, you purchased one contract (for 100 shares) of September $10 BHP call options. At that time, the price of a BHP share was $10.50 and the price of the call options on the Australian Stock Exchange (ASX) was $1.28. That is, at the time of entering the contract, you paid 100 * $1.28 = $128 for the right to purchase 100 BHP shares for $10 each at any time before the contract matures.
It is now September 20, which is the maturity date for September options, and the BHP stock price is $9. Will you exercise the option and, regardless, what is the payoff and profit from the option contract?
In this case, you would let the option lapse and no funds would change hands. You would clearly be unwilling to pay $10 per share by exercising the option when the stock is only worth $9. That is, the payoff is zero and the profit is –$128 (0-$128)
Exercising a Put Option
Suppose that on March 20, you purchased one contract (for 100 shares) of September $10 BHP put options. At that time, the price of a BHP share was $10.50 and the price of the put options on the Australian Stock Exchange (ASX) was $0.53. That is, at the time of entering the contract, you paid 100 * $0.53 = $53 for the right to sell 100 BHP shares for $10 each at any time before the contract matures.
It is now September 20, which is the maturity date for September options, and the BHP stock price is $12. Will you exercise the option and, regardless, what is the payoff and profit from the option contract?
In this case, you will not want to exercise the option: You would clearly be unwilling to sell BHP shares for $10 per share by exercising the option when the stock is actually worth $12. That is, the payoff is zero and the profit is –$53 ($0-$53)
Exercising a Put Option
Suppose that on March 20, you purchased one contract (for 100 shares) of September $10 BHP put options. At that time, the price of a BHP share was $10.50 and the price of the put options on the Australian Stock Exchange (ASX) was $0.53. That is, at the time of entering the contract, you paid 100 * $0.53 = $53 for the right to sell 100 BHP shares for $10 each at any time before the contract matures.
It is now September 20, which is the maturity date for September options, and the BHP stock price is $9. Will you exercise the option and, regardless, what is the payoff and profit from the option contract?
you would exercise the option. You receive $10 * 100 = $1,000 in return for 100 BHP shares (which are worth only $900)
Hence, the payoff from the option contract is $100 and the profit (net of the initial cost) is $47 ($100-$53)
Selling to Close
options over shares are traded on
the Australian Stock Exchange (ASX) (note that options can be exchange traded, as in the case of share options, but, in some other instances, are traded over the counter)
Selling to Close
All stock options on the ASX are
of the American type. Therefore, if the holder of the option so wishes, they may exercise the options at any time before maturity
Selling to close
An alternative way for the holder of the option to liquidate their option position is
An alternative way for the holder of the option to liquidate their option position is by issuing a sell to close order.
what is a sell to close order?
This procedure simply involves an option buyer selling their rights under the option contract to a third party.
Suppose, that on March 20, you purchased one contract (100 shares) of September $10 BHP call options when the BHP stock price was $10.50 and September $10 call price was $1.28. Also suppose that it is now August 20, still one month before maturity and that you want to cash out of your position. The BHP stock price is now $10.70 and the call option price is $0.84. There are two ways to cash out of this contract
–First, you may exercise the option. This will generate a benefit of $0.70 per option (you pay $10 for a share that is worth $10.70); or,
–Second, you may sell the option as a live contract by issuing a sell to close order.This will generate a benefit of $0.84. Issuing a sell to close order results in youroption position being extinguished and all of the rightsyou had under the option contract arepassed on to the subsequent buyer.
As with forward and futures contracts, option contracts can also be valued by
arbitrage
option valuation
what is Put-call parity
is a pricing relation between the underlying stock and put and call options written on the stock.
option valuation
For European put and call options with the same exercise price and maturity date put-call parity is given by:
is a pricing relation between the underlying stock and put and call options written on the stock.

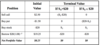
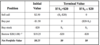
Suppose that European call and put options on Brambles with exercise prices of $20 and six months to maturity are selling for $2.50 and $1.50 respectively, that the Brambles stock price is $20, and that the riskless rate of interest is 8% p.a.
is put-call parity violated? If so, tabulate the strategy you would employ to make an arbitrage profit.
put-call parity is violated since c = 2.50 > p + S0 – X(1 + rf)–T = 2.25. The violation occurs because of any one or all of the following possibilities:
–The call is overpriced;
–The put is underpriced; and / or
–The stock is underpriced.