TIme Domain: Elementary Signals

Question 1

What is the unit step function u(t)?

Answer 1

u(t) is a function which is 1 for time greater or equal to zero.

u(t) is zero for time, t, less than zero

Question 2

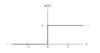
What are the two most common uses for the unit step function?

Answer 2

1. u(t) can be used to model a causal signal, which is a signal that is ‘turned on’ at time t=0.
2. u(t) can be used to check how a system responds to a sudden input known as the system step response.

Question 3

What is a rectangular pulse function?

Answer 3

A rectangular pulse function is defined to be 1 for a fixed time interval and is 0 otherwise

Question 4

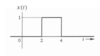
A pulse function, x(t) is defined to be 1 between the interval a < t < b. How can we express this as a function of two unit step functions?

Answer 4

x(t) = u(t - a) - u(t - b)

Question 5

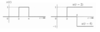
What is an impulse function?

Answer 5

A pulse function is also known as a delta function as is define as a function which is zero fot all time that is not zero and is very large near t=0.

The integral of an impulse function with respect to t is equal to 1.

Question 6

What is the general form of a CT complex exponential, x(t)?

Answer 6

A and λ are complex constants

Question 7

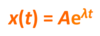
What are the 3 modes of behavior for a complex exponential?

Answer 7

1. Mode 1 - Real exponential
2. Mode 2 - Complex sinusoid
3. Mode 3 - Complex exponential

Question 8

What do we expect the graph to look like for a real exponential x(t) for the three cases where:

1. λ > 0,
2. λ = 0
3. and λ < 0?

Answer 8

1. x(t) increases exponentially as t increases which is known as a growing exponential.
2. x(t) simply equals the constant A.
3. x(t) decreases exponentially as t increases which is a decaying exponential

Question 9

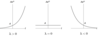
How can we express a complex sinusoid? (Hint: Euler’s)

Answer 9

x(t) = |A|cos(ωt + θ) + j |A|sin(ωt + θ)

Question 10

How can we express a complex sinusiod in which ω = 2π? (Hint: Euler’s)

Answer 10

Question 11

What is the euler’s formula for a complex exponential?

Answer 11

Let,

A = |A|e^(jθ) and λ = σ + jω

Question 12

What are the 3 modes of behaviour for a complex exponential, where:

1. σ > 0
2. σ = 0
3. σ < 0

Answer 12

1. σ > 0: sinusoid growing exponentially
2. σ = 0: sinusoid
3. σ < 0: sinusiod decaying exponentially

Question 13

When is the following function a real exponential?

Answer 13

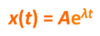
A and λ are both real

Question 14

When is the following function considered a complex sinusoid?

Answer 14

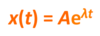
When A is complex (has real and j components) and λ is purely imaginary (only has j component).

Question 15

When is the following function considered to be a complex exponential?

Answer 15

When both A and λ are complex