Analysis: CT Systems

Question 1

What is a transfer function?

Answer 1

A transfer function H(s) is the relationship between output Y(s) and the input X(s), represented by:

Y(s) = H(s)X(s)

(A function that transfers the input X to the ouput Y)

Question 2

What is the equation for the transfer function?

Answer 2

H(s) = Y(s)/X(s)

Transfer function = Output/Input

Question 3

How do we find the impulse reponse of a system with transfer function H(s)?

Answer 3

By taking the inverse Laplace transform of H(s)

Question 4

What is the transfer function of a series interconnection?

Answer 4

H = H₁H₂

Question 5

What is the transfer function of a parallel interconnection?

Answer 5

H = H₁ + H₂

Question 6

What is a zero?

Answer 6

The roots of the numerator of a transfer function

Question 7

What is a pole?

Answer 7

The roots of the denominator of a transfer function

Question 8

When considering poles-zero map when is a system considered stable?

Answer 8

A system is stable if all poles lie in the left-half of the s-plane where σ < 0

Question 9

If we plot a zero-pole map of a transfer function, how can we evaluate the magnitude and phase at s=p?

Answer 9

Magnitude = (product of the distances of zeros to p) / (product of the distances of pole to p)

Phase = (sum of zero angles to p) - (sum of pole angles to p)

Question 10

How do we form the transfer function for steady state analysis?

Answer 10

s = σ + jω for the Laplace transform, but growth factor σ = 0.

This means s = jω

Then we must subsitute s = jω into the transfer function for evaluation

Question 11

How do we evaluate the steady state response from a pole-zero diagram?

Answer 11

By evaluating H(s) along the imaginary axis from complex poles/zeros to point s = jω.

Question 12

How do we identify areas of attenuation (steady-state)?

Answer 12

Frequencies near zeros get amplified as the length of the vector from those points to the pole is small (small denominator)

Question 13

How do we identify areas of amplification (steady-state)?

Answer 13

Frequencies near poles get attentuated as the length of the vector from those points to the zero is small (small numerator)

Question 14

How can we represent a second order transfer function?

Answer 14

Question 15

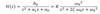
What is ω₀, ζ and K?

Answer 15

ω₀ = natural frequency

ζ = damping factor

K = gain

Question 16

What equation do we evaluate to find the step response?

Answer 16

Multiply transfer function by 1/s = unit step

Question 17

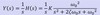
What is the method for finding the step response in the time domain from a transfer function?

Answer 17

Calculate the inverse Laplace Transform

1. Find the roots of the denominator polynomial (poles) and factorise
2. Use partial fraction expansion to express the sum of first order fractions
3. Use the Laplace transform table to revert to the time domain

Question 18

What is ζ = 1?

Answer 18

Critical damping

• roots (poles) will be a double real negative
• the step response takes the form of an exponential
• it has the fastest response without oscillations

Question 19

What is ζ > 1?

Answer 19

Overdamped

• poles are two real and negative poles
• step response has still has the form of a growing exponential but is slower

Question 20

What is ζ < 1?

Answer 20

Underdamped

• poles are complex
• the imaginary part of the poles indicates oscillation before coming to rest

Question 21

What is ζ = 0?

Answer 21

Undamped

• roots are purely imaginary
• system oscillates and does not come to rest