Thermal Physics Flashcards
(22 cards)
Internal Energy
The sum of the randomly distributed kinetic and potential energies of all its particles.
Some particles move faster than others so kinetic energy is randomly distributed.
They also have randomly distributed potential energies depending on their relative position.

Specific Heat Capacity
The energy needed to raise the temperature of unit mass of a substance by 1K without change of state.
Q = m c ςT

Specific Latent Heat
The energy required to change the state of a unit mass of a substance without a change in temperature
Energy change = mass of substance changed x specific latent heat
Q = m l

Latent Heat of Fusion
The amount of heat required to convert a unit mass of a solid into a liquid without a change in temperature
e. g. Ice to water (melting)
1. Energy supplied
2. Temperature increases
3. Particles gain energy
4. Temperature stops increasing and change of state occurs
Latent Heat of Vaporisation
The amount of heat required to convert a unit mass of a liquid into a vapor without a change in temperature
- Energy supplied
- Temperature increases
- Particles gain energy
- Temperature stops increasing and change of state occurs
Energy Changes between Particles
For a closed system, the total internal energy is constant.
Energy is constantly transferred through particle collisions, but the total internal energy doesn’t change.
The internal energy can be increased by heating or cooling a system, or by doing work e.g. changing its shape
If one of these changes occurs, the average kinetic or potential energy of the particles will change.
When a substance changes state, its internal energy changes but its kinetic energy stays the same, as only the potential energy is changed.
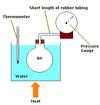
Continuous Flow Calorimeter
Continuous-Flow Heating Calorimeter
- when a fluid flows continuously over a heating element
- as it flows, energy is transferred to the fluid
- Allow water to flow at a steady rate until the water out is at a constant temperature
- Record the flow rate of the water and the time taken for the experiment
- Measure the temperature difference
- Record the current and potential difference
- Energy supplied Q = mc ςT + H (H is the heat lost to surroundings)
Specific heat capacity of the liquid (c) = [Q2 – Q1]/(m2 – m1)(θ1 – θo)

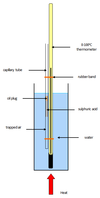
Finding the Specific Heat Capacity
- Weigh the substance and record its mass, m
- Record the initial temperature shown on the thermometer
- Switch on the heating element and the joulemeter
- After a certain amount of time, turn the heating element off
- Continue to watch the thermometer in case temperature continues to rise
- Record the maximum temperature
- Record the energy on the joulemeter
- Calculate the specific heat capacity
The Avogadro Constant
The avogadro constant is the number of atoms in exactly 12g of the isotope carbon 12.
Amount of Substance
The quantity of a substance measured in moles, n.
N = n x Na
Molar Mass
The molar mass of a substance is equal to the mass of one mole of the substance.
moles = mass/Mr
The Ideal Gas Equation
Combining all three gas laws for a constant mass of gas gives:
pV = nRT
pV/T = a constant
n = number of moles of the gas
R = molar gas constant (8.31)
T = temperature measured in kelvin
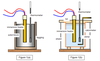
Boyle’s Law
P1V1 = P2V2
As pressure goes up, the volume goes down (temperature is kept constant):
If the volume of a container decreases, the rate at which particles collide with the walls increases, resulting in increased pressure.

Charles’ Law
V1/T1 = V2T2
As temperature increases, the volume increases (pressure is constant):
When air is heated, the particles will gain kinetic energy and there will be more frequent collisions on the walls of the container, forcing it to expand.
Pressure Law
P1/T1 = P2/T2
As temperature increases, the pressure increases (volume is constant):
When the temperature increases, the particles gain kinetic energy and collide more, exerting more force, and hence more pressure on the walls of the container.
Brownian Motion
The random motion of particles is a result of collisions with fast, randomly moving particles in a fluid.
Einstein explained that the pollen grains that Brownian noticed moving randomly were being moved by individual water molecules:
Heavier particles are moved with Brownian motion by smaller, lighter particles travelling at high speeds
This is evidence that the air is made up of tiny atoms or molecules moving quickly.
The Maxwell Boltzmann Curve demonstrates the distribution of kinetic energy between particles:

Maxwell Boltzmann Distribution
Shows the number of particles with a certain speed:
Area under the graph = number of particles
Boltzmann’s constant, k is equivalent to R/Na (molar gas constant/avogadro’s constant)
k = 1.38 x 10-23 JK-1
pV = NkT ⇒ equation of state of an ideal gas

Work Done In Energy Transfer
- For a gas to expand or contract at constant pressure, work is done as there is a transfer of energy
- When heat is added, it will expand.
- When heat is removed, it will contract as heat is transferred back to the surroundings
The work done in changing the volume of a gas at a constant pressure is equal to:
work done = pςV
Deriving the Kinetic Theory Equation
Kinetic theory links temperature to the speed of the molecules in the gas:
Increasing Pressure
- Particles with a greater mass, have a greater force of collision, so greater pressure is exerted
- Higher temperature particles move faster and have a greater force of impact and a greater number of impacts
- Greater number of particles leads to a greater number of collisions
- When the particles collide with the end of a box, the force on the wall is
Force on wall = mv2/x
Pressure = force on wall/area of wall
Pressure = mv2/V
When considering how many molecules, there are N times as many collisions for N molecules
Pressure = Nmv2/V
On average, a 1/3 of the molecules are travelling in each direction
Pressure = 1/3 Nmv2/V
All the molecules are moving at different speeds
pV = 1/3 Nmv2

Kinetic Theory Of Gases Assumptions
- Gas has zero volume at zero temperature so the volume of the molecules is negligable
- Gas has zero pressure at zero temperature so thermal energy is its source of kinetic energy
- The gas has atoms or molecules which behave as elastic spheres with no long range intermolecular forces.
The Boltzmann Constant, K
Number of molecules: N = n x NA
n = N/NA
Ideal Gas Equation: pV = nRT
pV = NRT/NA
Ideal Gas Definition
- negligable volume
- collisions are elastic
- gas cannot be liquified
- no interactions between molecules (except in collisions)
- gas obeys the ideal gas law, boyle’s law, pressure law, charles’ law


