Further Mechanics Flashcards
(13 cards)
Circular Motion
Motion in a circular path at constant speed implies there is an acceleration and requires centripetal force
e.g. Cycling
- when riding for speed you pedal at top speed, and as long as the wheels aren’t skidding, the wheel in contact with the ground has a speed equal to the cyclists speed
- the faster the wheel spins, the faster the cyclist is going
- if the cyclists speed is constant then the wheels are spinning at a constant rate
- an object which rotates at a constant rate is in uniform circular motion
- C = 2πr so the time taken for one rotation is T, and the speed is:
V =2πr/T
- frequency = 1/T so:
V = 2πrf
Angular Displacement and Speed
For any object in uniform circular motion, the object turns through an angle of 2π/T radians per second - angular displacement is θ
θ = 2πt/T = 2πft
Angular speed is the angular displacement per second
ω = θ/t = 2π/T = 2πf
ω = 2πf
Angular speed = angular displacement/time
V = rω
Centripetal Force
Centripetal force is a force acting towards the centre
- the force always points to the centre of a circle
- tangential velocity
- would fly off in whichever direction tangential velocity is acting in
- Newton’s First Law*
- If a body is accelerating it must be subject to a resultant force
- Newton’s Second Law*
- The direction of the resultant force and the acceleration must be the same
Therefore, centripetal acceleration requires a resultant force directed towards the centre of the circular path
F = mv2/r
F = mω2r
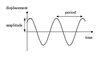
Free Oscillations
Free oscillations oscillate with a constant amplitude (no friction acting)
- only forces on it combine to provide restoring force
- there is no transfer of energy to or from the surroundings
Restoring Force
- For an oscillating object, the resultant force acting on the object acts towards the equilibrium position
- The resultant force is known as the restoring force
Forced Oscillation
If a system oscillates without a periodic force being applied, its frequency is called the natural frequency – there must be an external driving force
A periodic force can cause a system to oscillate, called a forced oscillation e.g. pushing someone on a swing they will go higher and higher - not always the right oscillation for that system
Damping
Damping is a measure of how quickly it is restored to the equilibrium
Heavy damping: damping is so strong that the displaced object returns to equilibrium more slowly, no oscillating motion occurs.
Light damping: amplitude reduces by the same fraction with each cycle. Each cycle takes the same amount of time.
Critically damping:oscillations are stopped after it has been displaced, released and returned to equilibrium, it stops in the quickest amount of time. It will never go onto the other side
There are dissipative forces which get rid of energy from the system

Resonance
When the applied force is equal to the natural frequency of the system, the amplitude becomes very large, proving that the damping is light
An object free to vibrate tends to do so at a specific rate called the object’s natural, or resonant frequency.
driving force = resonant frequency
- as the two approach each other, the system gains more and more energy and so vibrates with a rapidly increasing amplitude
Barton’s Pendulum
- Large pendulum is used to provide a driver frequency (periodic driving force) which makes smaller pendulums oscillate at the same rate
- The driver frequency is the natural frequency of the pendulum which is the frequency at which it would oscillate at without smaller pendulums
- D will be π/2 out of phase and have a natural frequency the same as the forced frequency
- A, B and C are in phase but have a much smaller amplitude
- E and F are π out of phase

Simple Harmonic Motion
SHM is oscillating motion in which the acceleration is always proportional to the displacement and the acceleration always acts in the opposite direction to the displacement
- Its acceleration is proportional to its displacement from the equilibrium position
- Its acceleration is directed towards the equilibrium position
- SHM is similar to circular motion, as the oscillations repeat, always returning to the start point
- Displacement is greatest at the end
- Velocity greatest in the middle
- Equilibrium point is in the middle, where the object remains stationary
- The mass continues to move through the equilibrium point as the momentum carries it through
e.g.
- mass hanging from a spring
- molecular osscilations
- pendulum or spring
- ruler oscillating on end of a bench

Mass on a Spring
When a mass is pushed to the left or pulled to the right of the equilibrium position, there’s a force exerted:
F = -kx
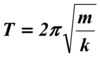
Simple Pendulum
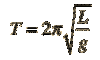
Displacement, Velocity, Acceleration Graphs
Energy Variation
Restoring Force
- For an oscillating object, the resultant force acting on the object acts towards the equilibrium position
- The resultant force is known as the restoring force
- If the restoring force is proportional to the displacement from equilibrium, the acceleration is proportional to the displacement and acts towards the equilibrium
- Therefore, the object undergoes SHM
Total Energy
E = 1/2 kA2
Et = Ek + Ep
Ek = 1/2 k(A2- x2)
The total energy remains the same as we assume that all potential energy is converted to kinetic energy
- if damping is applied, the total energy line will slope downwards
- In the space of one period for the displacement time curve, there are two waves for the energy (double the number of peaks), it becomes a sin2 graph that is all positive.



