The complexity of neural networks in the brain Flashcards
(10 cards)
What are the circuit and network activities?
It is the result of multiple sinusoidal waves that influence each other. It can be rewritten as the sum of sinusoidal functions.
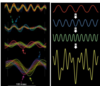
What does the Fourier transform make?
It can integrate all different waves into one. So the sum of sinusoidal functions defines a circuit and network activity. It transforms from the time domain to the frequency domain.

Is neural activity always periodic?
No it can be aperiodic.
How periodic and aperiodic neural activities can be described?
In a phase space.
Remember that oscillating activity is like a phasing rotator. The phasing rotator is described in the phase space and corresponds to the burst of the neuron.
Each 360-degree turn in phase space corresponds to a burst of a neuron.
Dynamical systems can be described in phase space: a mathematical space with independent coordinates representing the dynamic variables needed to specify the instantaneous state of the system.

When depicting circular motion in phase space they converge on a specific point. How it is called?
Circle around the focal point or attractor state.
It is a trajectory or point in phase space to which the system will converge.

How neural activity of an open non-equilibrium system can be described?
As dynamic nonlinear phase transitions of attracted states.
Dynamical systems (neural circuits and networks) operate near instability. What does it mean?
It responds rapidly with a large flexible repertoire of sensory and motor patterns. This is obviously important, especially for behaving animals.
What is an attractor?
Activity changes of dynamical systems can be described by attractor states: a trajectory or point in phase space to which the system will converge from a set of initial coordinates; a nonlinear system may have more than one attractor.
What is Lorenzo attractor?
Also called the butterfly effect. A very specific form of an attractor and its description in phase space.
Transitions through attracted states can occur.
What does the Lorenz attractor have to do with systems in neuroscience and brain function?
Activity (and behaviour) can be describe as dynamic, nonlinear phase transitions of attractor states.


