Target Test Math Cards Flashcards
What should you NOT do when working with average rate questions that involve multiple rates?
Do not try to get the overal average rate the by averaging the individual rates together, this assume each rate has the same amount time and neglects the fact that the object may have travelled at rates for differing amounts of time.
How do you solve these questions?
Using the converging rate equation and substituting in the rate/time formula.
The answer is 144
What is a neat way of solving the time to catch up and pass rate questions?
When can you not use this equation?
Time = ∆Distance / ∆Rate
Where the change in distance is extra distance the faster object has to travel over the slower one.
And the change of rate is the rate of the faster object minus the slower object.
You clearly not use this equation when there is no change in distance, i.e. the distance travelled by both is the same.
If you have two integers p and q and you know their LCM and GCF, what do we know about the value of p*q?
We know that GCF * LCM should contain all the factors in p and q.
Therefore GFC * LCM = p*q
In convering rate problems, what do the time and distance represent in the formula?
Time represents the time taken for two objects to converge.
The distance is the distance between the two objects before they start converging.
How are each of these lines Named?
Parallel lines intersected by a transversal: how are all the angles related?
What’s an important relation to remember about angles and their associated sides?
The largest angle is always opposite the longest side of the triangle; the smallest angle is opposite the shortest side of the triangle. In addition, equal sides will always be opposite equal angles.
Remember though, equal angles between triangles, does not mean the sides are the same, that really is more dependent on the rest of the triangles structure.
Given any polygon, when taking one exterior angle at each vertex, the sum of the exterior angles adds up to what value?
360º
What do we know about the relation between an exterior angle and the two remote angles within a triangle?
An exterior angle of a triangle is equal to the sum of its two remote interior angles.
Triangle Inequality Theorem
In any triangle, the sum of the lengths of any two sides of the triangle is greater than the length of the third side, and the difference of lengths of any two sides of the triangle is less than the length of the third side.
What is a scalene triangle?
A triangle where each side is a different length.
What are the most common Pythagorean triplets you should know?
The 3-4-5 and the 5-12-13 triangles.
If you see a triangle with side 9 and side 12, what should you think?
What are the 2x and 3x multiples of the 5-12-13 triangle?
9 and 12 are multiples of 3 and 4, therefore the triangle is a 3-4-5 triangle and the hypotenuse is 15.
The 2x and 3x mutliples are:
{10,24,26}
{15,36,39}
What is needed for these two triangles to be similar?
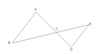
If angle A and D are the same then they are similar.
What condition do these triangles need to be similar?
If side ED is parallel to side BC.
What do these triangles need to be classed as similar?
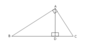
They are similar if the largest triangle ABC has a right angle and AD is the alitiude drawn from the right angle to the hypotenuse.
