General Math Cards

Question 1

What are the outcomes when Adding and Subtracting Even and Odd numbers?

Answer 1

Even ± Even = Even

Even ± Odd = Odd

Odd ± Odd = Even

Question 2

Outcomes when Multiplying Odd and Even numbers?

Answer 2

Question 3

How can you figure out if something is divisible by 3?

Answer 3

If the sum of the digits in a number add up to a value that is divisible by 3, then the number itself is divisible by 3.

Question 4

What is a trick to figure out if a number is divisible by 4?

Answer 4

That the last two digits of a number, and if this value is divisible by 4 then you know the whole number itself is divisible by 4.

Question 5

How do you know if a number is divisible by 5?

Answer 5

Just needs to have a 5 or 0 at the end…

Question 6

How do you figure out if a numebr is divisible by 6?

Answer 6

If a number is divisible by 2 (even) and 3 (the sum of all digits is divisible by 3) then you know that the number is divisible by 6.

Question 7

How do you figure out if a number is divisible by 8?

Answer 7

If the last three digits form a number that is divisible by 8.

Question 8

How do you figure out if a number is divisible by 9?

Answer 8

If the sum of the digits is divisible by 9 then the number itself is divisible by 9.

729 / 9

(7+2+9) / 9

18/9

Which is 2 so 729 is divisible by 9.

Question 9

How do you figure out if a number is divisible by 11?

Answer 9

If, when writing the signs -+-+ alternatively between the digits, the sum result is value divisible by 11.

Question 10

What are all the prime factors up to 50?

Answer 10

2, 3, 5, 7, 11, 13, 17, 23, 29, 31, 37, 41, 43, 47

Two is the smallest prime number and its the only that’s even, the rest are odd.

Question 11

What is something to remeber about the odd even relationship of prime numbers?

Answer 11

Two is the smallest prime number and its the only that’s even, all the rest are odd.

If they were even they would be divisible by 2.

Question 12

Is 1 a prime number?

Answer 12

It isn’t because it cannot be divided by two different factors.

Question 13

Are 51 and 91 prime numbers?

Answer 13

No.

51 is 3 * 17

and

91 is 7 * 13

Question 14

Prime Numbers: An integer can only be divided by?

Answer 14

1

itself

its prime factors

and integers created by multiplying some of its prime factors with other prime factors.

Question 15

When figuring out if a number is divisible by a set of numbers given, what do you need to remember?

Answer 15

That you can use the prime numbers to multiply into different multiples as many times as they appear when factoring down.

For example, if there are three 2s from factoring 120 down you can use 2 three times to create new factors.

Question 16

What technique can we use to figure out whether a number is prime?

Answer 16

Technique: if a number is not divisible by any prime number smaller than its root then its a prime number. If it is divisible, it is not prime.

Once you know the root, and figured out out all the prime numbers below it, divide the original number (i.e. before the root) by the primes and if they don’t divide the number itself is prime.

Question 17

How do we calculate the root of a number without a calculator? For example, the square root of 71.

Answer 17

By memorizing the mutliplication table we can estimate the root between the common values we do know.

With 71 we know that 8*8 is 64 and 9*9 is 81, so we know the root of 71 lies in between 8 and 9.

Question 18

What is the best technique to find the GCF between two numbers?

Answer 18

1. List out all the prime factors of both numbers
2. What prime factors are in common? In what number do the appear least? Get all prime factors and list the prime number in the quantity where it appears least.
3. Now multiply the prime factors by eachother to get the GCF.

The Greatest Common Factor is the largest factor that divides evenly into all numbers in a set.

Question 19

What is the fact technique to find the Least Common Multiple (LCM) between two numbers?

For example for 33 and 36

Answer 19

1. List out all the prime factors of both numbers
2. Add all the prime factors to one list but importantly list the common prime factors in the quantity where they appear most, do not add them double. Any prime factors that are not common are just listed as is.
3. Now multiple all the factors together to get the LCM

The prime factors of 33 are 3,11 and the prime factors of 36 are 2,2,3,3. The resulting list is 2,2,3,3,11. Multiplying this out gives: 396

Question 20

Data Sufficiency: General Answer Choices Structure

Answer 20

1. A - picking statement A
2. B - picking statment B
3. C - Combined, combining information would be enough to answer the question.
4. D - Divided / or, each one on their own is enough to answer the question.
5. E - E…impossible, even both combined together not enough information.

Question 21

What is the purpose of Data Suffiency questions?

Answer 21

The purpose is of data suffiency questions is not to solve the question but rather you have to figure out if the question can be solved.

You DO NOT have to answer the question, just whether or not you can come up with a answer.

Question 22

Can you trust sizes and proportions (such as apparent right angles) if theyre not explicility stated?

Answer 22

No, you can’t trust what you see.

An angle can be much larger or smaller than what it looks. Same goes for lines, areas or any other measurement.

Question 23

Is zero divisible any number?

Answer 23

Zero is divisible by any number, except itself.

Question 24

What is an acute angle? What is an obtuse angle? What is a reflex angle?

Answer 24

Acute = angle less than 90º

Obtuse = angle greater than 90º

Reflex Angle= angle larger than 180º but less than 360º

Question 25

What is a bisector?

Answer 25

A bisector is a line, line segment or ray that passes through the middle of a line segment or through the middle of an angle, and divides them into two equal parts.

Question 26

What is a neat way of remembering how the angles relate when parallel lines are crossed by another line?

Answer 26

F *U* N Where the angles in F and N are equal, large and small angles, while you can imagine angles in more squared U to be different but the sum of them both is 180º.

Question 27

Geometry: can straight lines be trusted when doing angle calculations?

Answer 27

Yes they can, but always double check.

Question 28

What is something you should really do when you first see a question?

Answer 28

_Read it carefully_, make sure you don't glaze over any important words and make sure you truly understand what they are asking.

Question 29

Is 0 rational?

Answer 29

Yes, because it can be written as a fraction. For example, 0/7.

Question 30

What are proper and improper fractions?

Answer 30

Proper fractions are fractions where the numerator is smaller than the denominator. Improper fractions are frations where the numerator is greater than the denominator. Improper frations can be equal to integers, i.e. the numerator can be divided without remainder by the denominator.

Question 31

What is a better way of adding fractions when both denominators produce a large number when multiplied?

Answer 31

You find the **Least Common Multiple** of both numbers. You do this by finding all prime factors, adding them to one list where the quantity of a factor is determined by where it occurs most, and finally taking the product of this list. Once found, you multiply the fractions, numerator and denominator, by the neccessary values to get them to the LCM.

Question 32

What are the decimals and percents of 1/8 and 1/6

Answer 32

1/8: 0.125 12 1/2 % 1/6: 0.1666... 16 2/3 %

Question 33

What's an important condition for this relation?

Answer 33

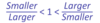
The values need to be positive. -ve vlaues would satisfy the greater than signs, but not be following the larger and smaller relation.

Question 34

Buying and Selling Products: What is the Cost price and what is the Expense? What is the selling price and revenue?

Answer 34

Cost price is the basic price demanded by the person who produced the good. The total cost of all the items bought by a seller is called the expenses. The selling price is the price for which the goods are sold to the customers. Revenue is the total sum recieved from selling items to customers.

Question 35

What is **simple** interest?

Answer 35

Simple interest doesn't take into account compounding and thus every year you receive or pay the same amount determined by the principal amount.

Question 36

With Data Sufficiency questions, what approach should you take?

Answer 36

You need to take the Logical approach

Question 37

What are the variables we need to know to solve simple interest problems? How many of those variables are needed in simple interest data sufficiency questions?

Answer 37

In simple interest questions we need to know 3 of the following 4: interest, principal, rate or time periods. With data sufficiency problems, knowing 3 of the 4 means there is _enough data_ to answer the question at hand.

Question 38

What is the external angle of a triangle equal to?

Answer 38

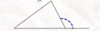
An external angle to a triangle is equal to the sum of the other two internal angles, the ones that it is not adjacent to.

Question 39

What do we know about the size of a triangles side and the associated opposite angle?

Answer 39

A larger side is always found opposite a larger angle.

Question 40

Triangles: the sum of any two sides is always greater than... The opposite?

Answer 40

The sum of any two sides is always greater _than the length of the third side_. A side of a triangle is always larger than the _difference of the other two sides._

Question 41

What is a acute triangle?

Answer 41

An acute triangle has three angles, each measuring less than 90º.

Question 42

What is a isosceles triangle?

Answer 42

An isosceles triangle has atleast two equal sides (called legs) with two equal angles opposite of them.

Question 43

What is the height of a triangle defined as?

Answer 43

The height is the shortest vertical line from the vertex to the base. The height is also referred to as the distance between the vertex and the base.

Question 44

What is the formula for the area of a triangle? What do you need to remember about obtuse triangles when it comes to this formula?

Answer 44

Base\*Height / 2 For obtuse triangles the height line is outisde the actual triangle.

Question 45

What is the ratio between the sides of a isosceles right angle triangles?

Answer 45

1:1:√2

Question 46

What is the Golden Triangle?

Answer 46

Also known as the 30-60-90 triangle is defined as the right angle triangle with one leg that measures 1/2 the hypotenuse. This leg is also the smaller of the two legs and therefore opposite the 30º angle. The ratio of the sides is 1:√3:2

Question 47

What do we know about two triangles with they have all the same sides (S-S-S)?

Answer 47

If all three sides are the same, they are identical.

Question 48

What do we know about a triangle with two of the same side and the same exact angle between this sides?

Answer 48

They are indentical

Question 49

If two triangles have the same two angles and the same exact side between these angles, what do we know? What about if two triangles have two sides that are the same and the exact same angle _opposite_ the largest side?

Answer 49

In both cases the triangles are the same.

Question 50

Why do we only need two angles to determine of triangles are similar?

Answer 50

Because we can determine the last angle knowing that all angles add up to 180º.

Question 51

If you know the areas of two triangles, how do you figure out the proportion of the perimeter of both triangles?

Answer 51

√a:√b where a and b are the respective areas.

Question 52

When multiplying numbers in your head, what is something you cannot do? i.e. 24\*24

Answer 52

you can't just break up the number into parts in one line of products and break it up, e.g. 20\*20\*4\*4. This is wrong, do not do it. Instead if you're multiplying mentally, multiply each of the digits by each other, in other words, the ones digit with the tens, the tens with the tens and the ones with the ones.

Question 53

What is the equation for the area of a equilateral triangle?

Answer 53

Question 54

What do you have to remember about -3²?

Answer 54

The power of two is on the three and does not include the -ve, so the value is -9. If there power was applied to a -3 brackted, then it would be 9.

Question 55

x⁰ is? What is √0?

Answer 55

1 √0 = 0

Question 56

What are the main squares you need to memorise for the GMAT?

Answer 56

The hidden one at the bottom is 25²

Question 57

What are the merging rules for a to the root of c and b to the root of c, i.e. the same root?

Answer 57

Question 58

What is a quadrilateral?

Answer 58

A quadrilateral is a shape with four sides and four angles.

Question 59

Quadrilaterals: what is a diagonal defined as?

Answer 59

A segment that _connects two vertices_ is a diagonal.

Question 60

What is a trapezoid?

Answer 60

A trapezoid is a quadrilateral with just one pair of parallel sides.

Question 61

Quadrilaterals: How do you calculate the area of a kite?

Answer 61

Area = Product of diagonals / 2

Question 62

What are the important things you need to know about parallelograms?

Answer 62

Opposite angles are equal. The sum of the two sides that are adjacent, at the ends of the two sides, is 180º. The equation to calculate the area is =\> Base\*Height

Question 63

How do you calculate the area of a trapezoid? If you know one angle in trapezoid corner, how do you calculate the one above or below it? What do we know about opposite angles in a isoceles trapezoid?

Answer 63

The area is the average of the two parallel bases times the height. (sum\_of\_bases/2)\* height ---- Since the bases are parallel, the other angle is simply 180 minus the angle you know. ---- Opposite angles in a isoceles trapezoid add up to 180

Question 64

Other than side² what's another way of calculating the area of a square?

Answer 64

Diagonal²/2

Question 65

What do the KiDS quadrilaterals all have in common?

Answer 65

KiDS Kite Diamond Square Area = Product of diagonals / 2

Question 66

What do we know about two inscribed angles that face the same arc?

Answer 66

They are the same angle.

Question 67

What is the angle of an inscribed angle that faces the same arc as a central angle?

Answer 67

The inscribed angle is half the measurement of the central angle.

Question 68

How do arc angles relate to the amount of the circumference they take?

Answer 68

The bottom value is 30º =\> 1/12

Question 69

How do you calculate the area of a sector?

Answer 69

Area of a sector = x/360 \*πr²

Question 70

What is a sequence?

Answer 70

A sequence is a group of numbers (called terms) in a certain order with some sort of relationship between them.

Question 71

How many sides do pentagons and hexagons have?

Answer 71

Penta = 5 Hexa = 6

Question 72

What is the equation for the sum of the internal angles of a polygon? How would you find the internal angle of a regular polygon?

Answer 72

180(n-2) where n is the number of sides. An internal angle of a regular polygon is 180(n-2)/n

Question 73

What is the sum of the external angles of a polygon?

Answer 73

The sum of the external angles of any polygon is 360º.

Question 74

What is a _regular_ polygon?

Answer 74

A regular polygon is a polygon whos sides are all equal and whose angles are all equal. Like a traingle, square, regular pentagon, regular hexagon and regular octagon.

Question 75

What does it mean when a polygon circumscribes a circle? What about when a polygon is inscribed in a circle?

Answer 75

It means that the circumference of the circle touches all the sides of the polygon (all sides are tangent to the circles circumference). --- An inscribed polygon has all its vertices on the circumference of the circle.

Question 76

What is something we know about the angle of a quadrilateral if it's inscribed in a circle?

Answer 76

If a quadrilateral is inscribed in a circle, the sum of each two opposite angles is 180º, and also the other way around, if the sum of two opposite angles in a quadrilateral is 180º it can be inscribed in a circle.

Question 77

Counting Methods: When we have to count the possible combinations between two different groups without any limitations what can we do it to solve it?

Answer 77

You can just multiply the options., e.g. 4 of one group and 5 of another means 20 different combinations.

Question 78

Counting Methods: How many different ways can 5 people stand in a row?

Answer 78

You multiply the possible people you can choose for the 1st place, then from the remaining people how many you can choose for the 2nd place, etc. 5\*4\*3\*2\*1 = 120

Question 79

Counting Methods: What should we know if order doesn't matter?

Answer 79

When order doesn't matter, we divide the number results by k! (where k is the number of possible inner arrangments of any given selection).

Question 80

What are the two main values you need to remember to divide by when dealing with combination problems _where order doesn't matter_?

Answer 80

2 objects: We divide the number of options by 2! which is 2. 3 objects: We divide the number of options by 3! which is 6.

Question 81

When you're dealing with probabilities stemming from more than one object, what is a key thing you need to remember?

Answer 81

If there is overlap between the items, don't count the overlapped possibility twice. For example if you're trying to figure out the probability that you get a 1 on the first or second die (or both) you need to mindful of the fact that (1,1) occurs in both sets, and thus you need to remove 1/(6\*6) from the basic probability calculation you make.

Question 82

What is the equation for the surface area of a cylinder?

Answer 82

2πr² + 2πrh

Question 83

What is the median? What is the mode?

Answer 83

The median is the number that is in the middle of a list, half the numbers are larger, half are smaller. The mode is the value that occurs the most in a list.

Question 84

How do we calculate the standard deviation for a set of numbers in the GMAT?

Answer 84

1. Find the average 2. Find the difference between each of the items and the average 3. Apply the power of two to each of the differences individually 4. Now calculate the average of these differences, you now have the variance. 5. The standard deviation is the square root of the variance.

Question 85

What do ∩ and U mean?

Answer 85

∩ = means the intersection between two sets, so P(A ∩ B) is the equivalent of A and B happening. U = the set made by combining the elements of two sets.

Question 86

What are general things you need to be doing when solving Data Sufficiency problems?

Answer 86

Get used to cancelling out answers that are not possible. Write down the equations when possible. This will help you visualise whether you can solve it using one statment alone, need both or neither are sufficient. No need to solve the equations, you just need to get to the point where you realise that it can be solved or not.

Question 87

What's the difference between Combination and Permutation?

Answer 87

Combinations are used when the order in which the task is done does not matter. Permutations, in contrast, are used when the order does matter.

Question 88

If there is m ways to perform task 1 and n ways to perform task 2 and the tasks are _independent,_ how do you calculate the amount of ways both these tasks can be performed together?

Answer 88

You multiply m by n, m\*n. This is only the case if they're independent.

Question 89

What should we think of when we see a question that looks at choosing multiple items from multiple groups using the word 'or'?

Answer 89

That the events are mutually exclusive. There are x ways to accomplish event A and y ways to accomplish event B, and if A and B are mutually exclusive, then there are x + y ways to accomplish A or B.

Question 90

Combinations and Permutations: What do you have to do when a question states that some items must be chosen? What about when some items are not to be chosen?

Answer 90

When some items need to be chosen, you subtract that amount from the objects in the set as well as the potential number of objects to be selected (since these places are already taken). When some items are not to be chosen, you remove this value from the amount of objects/people in the set but the number of objects that can be selected for combination stays the same.

Question 91

What is an easier way to solve permutation problems without using the full equation?

Answer 91

The box and fill method Figure out how many objects can be selected, this forms the number of boxes. Then successively fill the boxes from the number of objects in the set subtracting down one by one. In other words, each box represents a choice to be made and you multiply the values to get the final number of permutations.

Question 92

When an object is x times as fast as a second object, how do you relate both rates? Similarly percentages of another objects rate?

Answer 92

given that the second object has a rate r, the other object would have a rate of x\*r. With percentages the rate would be (x/100)\*r.

Question 93

What is the best way of splitting up the Data Sufficiency answer choices?

Answer 93

A/D and then B/C/E If A doesn't work you can automatically cross out D as well.

Question 94

How many equilaterial triangles fit inside of a regular hexagon?

Answer 94

A regular hexagon can be divided into 6 equilateral triangles.

Question 95

What happens when a regular polygon is inscribed in a circle?

Answer 95

When a regular polygon is inscribed in a circle, the polygon divides the circle in arcs of equal length.