Practice Questions & Answers

Question 1

What is the main thing you need to remember about this question?

Answer 1

The answer is B.

You need to remember here that zero is neither positive nor negative, so statement I can’t be true because if any of the variables is zero the product of them all is zero.

Question 2

Factorial and division:

Answer 2

Question 3

Pick one of the following:

A) 2

B) 3

C) 5

D) 7

E) 11

What do you need to remember about this question? (what is the main thing you learned?)

Answer 3

A square of an integer has each prime factor twice, since 392 is missing one 2 to be able to fully squared, y needs to be 2 to be able to x².

So remember, a sqaured number has twice the number of prime factors as the base number.

Question 4

Remainder Question

A) 3/4

B) 1/3

C) 5/8

D) 5/7

E) 7/8

What do you need to remember here?

Answer 4

You need to remember that the remainder is based on the numerator not the denominator…

Also you need to know to solve these remainder problems when they give you the final answer. The remaider will essentially be equal to R = (a/b) * b if a is smaller than b, which means that the remainder is equal to a.

Question 5

How do you approach this type of prime number question?

A) 0

B) 1

C) 2

D) 3

E) 4

Answer 5

You got to do prime factorisation, so practice breaking up numbers quick.

Question 6

What do you need to remember about this question?

A) 2

B) 6

C) 15

D) 16

E) 30

Answer 6

Remember to clearly differentiate the variables. The GMAT sometimes tries to confuse you with similar looking variables. In this case 〈〈x〉〉 represents a different number to x, so you might as well right it as ‘y’. The 3 and 5 factors are not a feature of this ‘y’ variable, instead all we know that its bigger than x and it is even.

Question 7

Factors: How do you need to approach this question?

A) A!

B) B!

C) Combined

D) Divided

E) E..imposssible

Answer 7

For 8 to be a factor, the brackets need to have the factors 2 and 4 or one of the brackets needs to have the factor 8. We determine this from the information given.

Question 8

If n = 20!, then n is divisible by

A)

B)

C)

D)

E)

Answer 8

Question 9

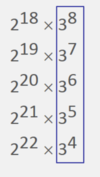
If {n} is the smallest integer greater than n, what is the value of {1.5} - {0} - {-1}

Answer 9

Question 10

The product of four consecutive integers is always:

What do you need to remember with this question?

Answer 10

0 is divisible by any number that’s why ‘divisible by 8’ is right.

On the other hand, 0 is not positive or negative.

Question 11

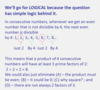
If x/6 is a positive integer, does x have more than two different positive prime factors?

(1) x/4 is a positive integer
(2) x/9 is a positive integer

What do you need to remember with this question?

Answer 11

What you need to remember is the wording and to really pay attention to it. They want to know if there are more than 2 positive prime factors, not whether there are 2 prime factors.

Question 12

What has this question taught you about how you should approach data suffiency questions?

A!

B!

Combined

Divided

E..impossible

Answer 12

You need try each statement in isolation, if neither work, try to see if they work by combining, if not its E.

Question 13

Data Suffiency: What did you learn with this question?

Answer 13

That zero is considered even (and an integer). More specifically, a number ending in zero is even and therefore has to be considered in this case.

10*10 is 100, thereby complying with the second statement. Thus knowing that two digit numbers which end with 6 also end with 6 when squared doesn’t give us all the information to answer the question.

As result, we need both statements to be able to answer the question.

Question 14

Data Suffiency: Geometry

Answer 14

Apparently you only need to have statment (1) because it shows that the diagonal lines are parallel and tells us that x = z, which then allows us to calculate y based on the fact, that the small + large angle in these intersections is equal to 180º.

Question 15

Data Sufficiency: Geometry

A!

B!!

Combined

Divided

E..impossible

Question 16

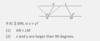
Which two lines are parallel?

a and b

a and c

a and d

d and e

d and f

Answer 16

Question 17

In the figure, if x and y are integers, how many different values can x have?

0

1

2

4

6

Answer 17

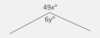
You need to consider 6y here aswell!

So go thorugh the x values and think logically what values of y will work given the coefficient 6.

Question 18

12 is 15% of x. What is x?

What is the best method for solving these?

Answer 18

12/x = 15/100

Solve for x.

Question 19

Which is large m or n?

Answer 19

The answer is C.

It can’t be just A because if m and n are both negative, the inequality could work but it will erroneously pick

Question 20

Which letter represents the same positive digit in the decimal form of 1/11 and 1/13?

Answer 20

The answer is d

Make sure to read the question properly.

Question 21

The population of two cities, A and B, in thousands, is 142 and 61, respectively. The population of city A is approximately what percent greater than the population of city B?

What can you do to solve these sorts of questions?

Answer 21

You can simplify to the numbers so that easier to work with an you can get a close estimate of what the answer would be.

Question 22

How should you approach this question?

Answer 22

If the numbers are too crazy to mentally calculate you need to make estimations. In this case specifically you need to calculate the extremes of the reciprocal sum for a, all of them 1/11 and all 1/20.

Question 23

What did you do wrong here?

Answer 23

You didn’t read the question properly. They are asking for the percent of smoking members that are non-cigar smokers, not the percent of the total congress. You need to do 21/70.

Question 24

When r is rounded to the nearest integer, the result is 1? Is r an integer?

Answer 24

Question 25

What is possibly a better way of solving this question rather than going straight to the equations to solve for r?

Answer 25

Simply use the possible answers given to you to plug in values and see what gives you the right outcome.

Question 26

If each of the sides of ABC is enlarged by x, then its area will become how many times larger?

Answer 26

D

The change in the area is equal to the change of the sides squared: x²

Question 27

Data Sufficiency: In the figure, what is AB?

Answer 27

We know two angles are the same, there we can conclude that the side AB is equal to BC.

Question 28

Solve for z

What do you have to remember in this question?

Answer 28

You need to indentify the second equation which can be formed using the triangle DEC. Using this equation you can tranpose the equation into the other one through y.

Question 29

How many different triangles can be drawn…

Answer 29

Question 30

In the figure, BD is?

Answer 30

The answer is D.

Question 31

What is AF?

Think of the most effective way to solve this.

Answer 31

You need to use the fact that the smaller inner triangle is indentical to the larger whole triangle expect for proportion.

Question 32

What is the area of the triangular region ABC (the whole triangle)?

Answer 32

You could have gone for the precise approach using variavles and the 3,4,5 triangle, but the most effective approach is the logical one.

Question 33

Data Sufficiency: What is the area of ADE?

Answer 33

You can also anwer the question by concluding that the smaller triangle can fit three more times into the larger triangle, i.e. four of the ADE fit in ABC.

Question 34

What is 7/√7 ?

Similarly, √7/7

Answer 34

√7

This goes for any value.

√7/7 = 1/√7

Question 35

What is the number of 5-ball combinations that can be pulled out of a bag which holds 7 balls in different colours?

Answer 35

We’re picking 5 out of 7, so there are 7*6*5*4*3 ways to do so.

However, since order doesn’t matter, there are 5*4*3*2*1 ways of picking the same balls (that is, in a different order). We then divide one by the other and get (7*6*5*4*3)/(5*4*3*2*1) = 42/2 = 21

Question 36

How do you solve these rate problems involving averages?

Answer 36

You can’t just average it, you need to use total_distance/(t₁+t₂) and replace total time with the individual rate equations D/r where D is distance r is rate.

Question 37

How many digits are in this number?

Answer 37

The answer is 19.

The key here is remember the 5^x * 2^y relaionship to make trailing zeros. Knowing that makes these seemingly complicated question a lot easier to solve.

Question 38

Linear And Quadratic Equations: Data Sufficiency Problem

A!

B!

Combined

Divided

E..impossible

Answer 38

This is a trick question and the answer is A.

Just because you get an equation that has two unkowns doesn’t mean it automatically rules out the one option alone, you need to consider logically if the expression can take multiple different values or if it in fact limits one of the variables to one value due to logic.

Question 39

Work Problem: How long will it take for them to paint the house together?

Answer 39

The main equation you need to remember here is that:

work_total = work_jason + work_john

Where work is equal to rate*time. The individual rates of the Jason and John come out to 1/6 and 1/4.

Which comes out to:

1 = (1/6)t + (1/4)t

Question 40

Overlapping Sets: Data Sufficiency

A!

B!

Combined

Divided

E..impoissible

Answer 40

Create a table and test out both possibilities separately and then together.

The answer is C.

Question 41

Inequalities and Absolutes: Is a/c > c/d?

What do you need to remember about this question?

A!

B!

Combined

Divided

E..impossible

Answer 41

Multiplying an inquality by a negative flips the sign, therefore we need to know whether a,b,c,d are negative or not.

The answer is C.

Question 42

Roots and Exponents: Solve for y

What do you need to remember from this problem?

Answer 42

Look to make the decimals easier to deal with, convert them to ‘integers’ using scientific notation. The handling of the values and 10s becomes a lot easier once you do that.

Question 43

Combination and Permutations

Answer 43

The answer is 18.

The key thing here is remember the equation:

nC_k = n! / K!(n-K)!

Where n is the number of possible choices and K represents the number of choices in a combination.

Question 44

General Words Problems: Simple interest comparison

Answer 44

Don’t overthink this one. You simply need to right down the equations for each year up to 8 and then solve the equation knowing the 5/4 relation.

Question 45

Geometry: what is the area bounded by the chord YZ and the arc YZ?

What are the main things you need to remember here?

Answer 45

The relations and equations you need use:

30-60-90 triangles has the following relation x:x√3:2x

Arc length: 2pi*r*(θ/360)

Also importantly you need to remember that the central angle is 2 times the angle at YXZ, which you can then use to calculate the arc YZ.

Question 46

Weighted Average Problem

Answer 46

Remember in this case for the average you divide by the quantity of tickets.

Also, in these questions focus on writing down the equation and then solving for the unkown.

Question 47

Properties of Numbers Question

A!

B!

Combined

Divided

E…impossible

Answer 47

The thing you here is you need to remember the cyclicity of 7^x.

The units digit of the first for power is:

7¹ => 7

7² => _9

7³ => _3

7⁴ => _1

and the pattern repeats from here.

Question 48

Coordinate Geometry: What is the slope of line AB?

What did you learn from this question?

Answer 48

That if a line doesn’t intersect another said line, that means that their slopes are equal…

Question 49

Properties of Numbers: is mn < 0 ?

A!

B!

C

D

E…impossible

Answer 49

Just because the P is there doesn’t mean we can’t consider 2) to answer the question.

Question 50

Inequalities and Absolutes

What’s an important thing you learned (reminded of) here?

A!

B!

C

D

E

Answer 50

You cannot divide an inequality by an unkown variable (in this case dividing out z) because we don’t know whether it is -ve or not.

Answer is E

Question 51

Ratios: Data Sufficiency

Answer 51

Question 52

Ratios

Answer 52

Question 53

Geometry: Difference in the area of the two circles?

Answer 53

Question 54

Properties of Numbers: Data Sufficiency

Answer 54

Question 55

Properties of Numbers

Answer 55

Question 56

Statistics: Weighted Averages

Answer 56

Question 57

Combinations and Permutations: number of entities left open

Answer 57

Question 58

Combinations and Permutations: OR

Answer 58

Question 59

Combinations and Permutations: At least

Answer 59

‘At least’ problems normally require the addition of outcomes.

Question 60

Combinations and Permutations: Creating Codes

Answer 60

Question 61

Percentage Word Problem: A furniture dealer purchased a desk for $150 and then set the selling price to the purchase price plus markup that was 40 percent of the selling price. If the dealer sold the desk at the selling price, what was the amount of the dealer’s gross profit from the purchase and the sale of the desk?

1) $40
2) $60
3) $80
4) $90
5) $100

What do you need to remember in this question?

Answer 61

You need to remember to clearly read what they’re saying, underline key words in the question. In this case they’re saying the markup was 40% of the selling price.

Purchase price = 150
Selling price = x

150 + 0.4*x = x
0.6*x = 150
x = 250

Profit = 250 - 150 = 100 (E)

Question 62

If it took Carlos 1/2 hour to cycle from his house to the library yesterday, was the distance that he cycled greater than 6 miles? (Note: 1 mile = 5280 ft)

(1) The average speed at which Carlos cycles from his house to the library yesterday was greater than 16 feet per second.
(2) The average speed at which Carlos cycles from his house to the library yesterday was less than 18 feet per second.

A!

B!

Combined

Divided

E..impossible

What did you learn about this problem?

Answer 62

Learnt that it is really important to use the distance = rate * time equation with these problems, you cannot just average.

(1) Avg speed > 16fps
So distance covered > 16*1800 feet = 28800feet or about 5.45miles
So distance > 5.45 miles
Not sufficient

(2) average speed < 18fps
So distance < 18*1800 feet or about 6.14miles
So distance < 6.14miles
Not sufficient

(1)+(2) Distance is between 5.45 and 6.14 miles
Not sufficient to say if it is > 6 miles

Answer = E

Question 63

In a stack of boards at a lumber yard, the 20th board counting from the top of the stack is immediately below the 16th board counting from the bottom of the stack. How many boards are in the stack?

A. 38
B. 36
C. 35
D. 34
E. 32

Answer 63

There are some number of boards stacked.

20th board from the top is immediately below the 16th board from the bottom:

1
2
3
.
.
. 16
20 15
14
13
.
.
.
3
2
1

As you can see 20th board from the top is immediately below the 16th board from the bottom. The total number of boards 20(red)+14(blue)=34.

Answer: D.

Question 64

On the number line, if the number k is to the left of the number t, is the product kt to the right of t?

(1) t < 0
(2) k < 1

A!

B!

C

D

E..impossible

What mistake did you make?

Answer 64

The answer is A.

1. t is less than 0

T is negative and K is to the left of T so K is negative as well

negative*negative = positive

and any positive will be to the right of t when it’s negative

A is sufficient

2. k is less than 1

if T is 10 K could be 1/2 and kt would be to the left of T
if T is -1 K could be -2 and kt would be to the right of T

Insufficient

The mistakere here was that you did not consider that K could be a fraction, i.e. 1/2. Unless they say you’re only dealing with integers, consider fractions as well.

Question 65

What’s a really important thing you need to remember about data sufficiency questions?

Answer 65

You need to consider each statement independently. You need to test them by themselves first. Remove the other statement of your mind temporarily when you’re working on one.

This is realy important because you’ve consistently chosen C when it was either A or B.

Question 66

If the sum of the three different numbers is 54, what is the largest number?

(1) The largest number is twice the smallest number.
(2) The sum of the two smaller numbers is 30.

A!

B!

C

D

E

Answer 66

Question 67

Each of the students in a certain class received a single grade of P, F,or I.What percent of the students in the class were females?

(1) Of those who received a P, 40 percent were females.
(1) Of those who received either an F or I, 80 percent were males.

Answer 67

We are given that each of the students in a certain class received a single grade of P, F, or I. We can let p = the number of students who received P, f = the number of students who received F, and i = the number of students who received I. Thus, the total number of students in the class is p + f + i. We need to determine the percentage of students who were females.

Statement One Alone:

Of those who received a P, 40 percent were females.

This means 0.4p students are females. However, since we know neither the values of p, f, and i nor the percentage of students who received an F or I, statement one alone is not sufficient to answer the question.

Statement Two Alone:

Of those who received either an F or I, 80 percent were males.

This means 20 percent of the students who received either an F or I were females. In other words, 0.2(f + i) students are females. However, since we know neither the values of p, f, and i nor the percentage of students who received a P, statement two alone is not sufficient to answer the question.

Statements One and Two Together:

From the two statements, we can say that the percentage of students in the class who were females is:

(0.4p + 0.2(f + i))/(p + f + i) x 100

However, since we don’t know the values of p, f, and i, we can’t determine the numerical value of the expression above. Statements one and two together are still not sufficient.

Answer: E

The key thing here is too many unknown variables.

Question 68

If n is a positive integer and the product of all integers from 1 to n, inclusive, is a multiple of 990, what is the least possible value of n?

A. 10
B. 11
C. 12
D. 13
E. 14

Answer 68

We are told that n!=990∗k=2∗5∗32∗11∗kn!=990∗k=2∗5∗32∗11∗k –> n!=2∗5∗32∗11∗kn!=2∗5∗32∗11∗k which means that n!n! must have all factors of 990 to be the multiple of 990, hence must have 11 too, so the least value of nn is 11 (notice that 11! will have all other factors of 990 as well, otherwise the least value of n would have been larger)..

Answer: B.

So to be a multiple it must have all the factors of 990, this is only achieved if n is at least 11.

Question 69

Rate problems: Two objects leaving at different times

Answer 69

Question 70

Rate Problems: Converging - Data Sufficiency

A!

B!

C

D

E..impossible

Answer 70

The key here is to remember the logic of Vladimir having travelled 2/3 of the distance by 10mins, and thus the time to reach the house can be determined.

Question 71

Rates: Catch-up problem

Answer 71

In this case tom’s time gets 1/2 hour more to the time, as thats the extra amount of time he travels.

Question 72

Rate Problems: Data Sufficiency

What did you mess up here and what do you really need to remember?

Answer 72

You glanced over the first statement and missed that it said greater than 50. Always read the questions properly and don’t glance over!

Question 73

Geometry: Data Sufficiency

Answer 73

Question 74

Rates: Data Sufficiency

A!

B!

C

D

E..impossible

Answer 74

Question Stem Analysis:

We want to know whether he can drive 550 miles on the full take of gas. From the initial information given, we don’t know the fuel capacity nor the fuel efficiency of the car.

Question 75

Geometry: Data Sufficiency - Angle/Side relations

Answer 75

Question 76

Geometry: Exterior Angles

Answer 76

Question 77

Geometry: Data Sufficiency - Exterior and Interior Angles

A!

B!

C

D

E..impossible

Answer 77

Question 78

Geometry

Answer 78

Question 79

Geometry

Answer 79

Question 80

Geometry: what is the area of the parallelogram?

Answer 80

Question 81

Geometry: Relations between sides

Answer 81

Question 82

Geometry: Rate Question

Answer 82

Question 83

Geometry: Ratios

Answer 83