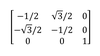Symmetry Flashcards
Number of faces on a cube?
6
Number of vertices on a cube?
8
Number of faces on a tetrahedron?
4
Number of faces on an octahedron?
8
Number of vertices on a tetrahedron?
4
“Procedure to Determine”
C<strong>2v</strong>
“Procedure to Determine”
Not a special group
C2 (yes, principal axis)
No ⊥C2
No σh
2σv
Chiral Point Groups
Cn ,D<b>n </b>T, O, and I groups only
All chiral molecules are polar
True or False
False
(e.g. Molecules in the Dn point group are chiral but not polar.)
Chiral Molecule
Molecules that lack an improper rotation axis
“Procedure to Determine”
C Point Groups
“Procedure to Determine”
Not a special group
No n⊥C2 to principal axis
“Procedure to Determine”
D Point Groups
“Procedure to Determine”
Not a special Group
n⊥C2 to principal axis
“Procedure to Determine”
D<strong>5d</strong>
“Procedure to Determine”
Not a special group
C5 (yes, principal axis)
5 ⊥C2
No σh
5σd
“Procedure to Determine”
C<strong>∞V</strong>
“Procedure to Determine”
Linear (Yes)
No ⊥C2
“Useful Matrices”
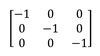
“Useful Matrices”
i
“Point Groups”
Bent corresponding point group
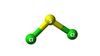
C2v
“Point Groups”
SeeSaw corresponding point group
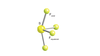
C2v
“Point Groups”
Square Planar corresponding point group
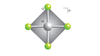
D4h
“Point Groups”
T-Shape corresponding point group
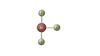
C2v
“Point Groups”
Trigonal Bipyramidal corresponding point group
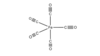
D3h
“Point Groups”
Trigonal Planar corresponding point group
D3h (SO3)
C2v (Acetone)
Cs (Methyl formate)
“Point Groups”
Trigonal Pyramidal corresponding point group
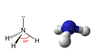
C3v
σperp and σh are equivalent types of mirror planes?
True or False
False
“Matrix Characters”
χ(S1 )
1
“Matrix Characters”
χ(σ )
1
“Matrix Characters”
χ(i)
-3
“Matrix Characters”
χ(C3)
0
“Matrix Characters”
χ(C2)
-1
“Useful Matrices”
χ (C2)
“Useful Matrices”
S4(z)
“Useful Matrices”
“Useful Matrices”
σh
“Useful Matrices”
“Useful Matrices”
C<span>n</span>(x)
“Useful Matrices”
“Useful Matrices”
C<span>n</span>(z)
“Useful Matrices”
“Useful Matrices”
C<span>3</span>(z)
“Useful Matrices”
“Useful Matrices”
C2(z)
“Groups”
C Point Group
“Groups”
No ⊥ C2 to principal axis
“Groups”
D Point Group
“Groups”
Not a special group
n ⊥ C2 to principal axis
Number of vertices in an octahedron
6
5 Platonic solids
“Operator”
E
“Operation”
The identity operator is the “do nothing” operator. All points remain at their original position.
“Operator”
i
“Operation”
Projects each atom through the center of symmetry to its negative xyz position.
“Operator”
σh
“Operation”
A mirror plane perpendicular to the principal axis.
“Operator”
Sn
“Operation”
A combination of Cn followed by σperp yields an improper rotation
“Operator”
Cn
“Operation”
A n-fold [360º/n] clockwise rotation about an axis
Operations with
axial symmetry elements
Cn and Sn
operations using a point symmetry element
E and i
