Simple Linear Regression

Question 1

Assumptions for Simple Linear Regression

Answer 1

Data must be continuous, interval or ratio scale, normally distributed and no significant skewness.

Question 2

Determining equation of a straight line

Answer 2

Y = a + bX

Question 3

Least-squares criterion

Answer 3

Regression line is fitted with reference to the difference between the line and individual data points.

Question 4

Residual

Answer 4

Differences between the data point and the regression line (the unexplained variance)

Question 5

Variance

Answer 5

Sum of squares/degrees of freedom.

Question 6

Coefficient of Explanation (r²)

Answer 6

Regression sum of squares of Y/total sum of squares of Y. The proportion of variance that is explained by the model. Regression coefficient or scatter plot indicates positive/negative relationship.

Question 7

Standard Error

Answer 7

Simply the Squared root of theunexplained variance.

Question 8

Calculating Confidence/prediction intervals

Answer 8

We can distinguish between confidence intervals around the line itself and the prediction itself and the prediction intervals that describe the estimates to which estimates of Y vary about the line. The prediction intervals are larger and reflect the collective uncertainties of scatter and errors in sampling a and b.

Question 9

Standardised Residual

Answer 9

Residuals are important because their character has important implications for the regression model. Their magnitude contributes to prediction limits.

Question 10

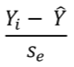
Homoscedasticity

Answer 10

For a model to be wholly reliable, the residuals should be distributed normally about the line. A requirement of homoscedasticity is that the degree of scatter should not vary greatly along the range of X.

Question 11

Heteroscedastic

Answer 11

For a model to be wholly reliable, the residuals should be distributed normally about the line. If it is not fulfilled the data is said to be heteroscedastic and the regression equation may be unreliable for some purposes.

Question 12

Autocorrelation

Answer 12

There should be independence between residuals and, consequently, no autocorrelation between them. Autocorrelation is indicated by either long runs of positie or negative residuals along the regression line, or, on the other hand, by rapid and regular fluctuations of residuals.

Question 13

Measures of autocorrelation

Answer 13

Durbin-Watson d-statistic. Based on the sequence of residuals so that: d = sum of successive squared differences/sum of sqaured residuals.

D-W value - indicate whether to accept or reject null hypothesis. 0.-1.475 indicates positive autocorrelation and 2.5-4.0 indicates negative.

Question 14

Non-Linear Regression

Answer 14

There are a number of bivariate relationships in Geography in which incremental changes in the predictor variable (X) are not accompanied by correspondingly uniform changes in the dependent variable (Y). Such relationships are said to be linear and are summarised by curves.

Question 15

Difficulty that lies in non-linear regression

Answer 15

There are many possivle forms of non-linear relationships.

Question 16

Exponential curves use the universal constant of

Answer 16

2.7182

Question 17

Partial regression coefficients

Answer 17

Represent changes in slope as X increases and are scale dependent.

Question 18

Non linear regression power curve

Answer 18

Equation is Y = aX^b