Multiple Regression

Question 1

Multiple regression allows

Answer 1

Hypotheses of no explanation of the dependent variable to be tested, and the nature of variable interactions to be explored by objective methods.

Question 2

Multiple regression attempts to

Answer 2

Predict the variation in a single dependent variable (Y) on the basis of two or more predictor terms.

Question 3

Multiple regression equation

Answer 3

Y = a+b₁X₁+b₂X₂+….b_nX_n+-e

Question 4

Scatter of points represented in graphical form

Answer 4

This cannot be done in the multivariate case in which each variable requires an axis for its representation. The principle of adopting the least-squares criterion remains important, and is adopted to define the best-fit surfaces through n-dimensional space. This concept can be illustrated by the case of two predictors and one dependent variable.

Question 5

Problem in multiple regression

Answer 5

We shouldn’t be tempted into assessing the importance of the each predictor by reference to its partial regression coefficient, and large values do not imply greater importance. Such comparisons are best made through the medium of beta weights.

Question 6

When our initial interest lies with the explanatory capability of the model as a whole this can be found from

Answer 6

The Multiple coefficient of explanation (R²), which is linked to the multiple correlation coefficient. The latter is a direct counterpart to the simple correlation coefficient but measures the association between the dependent variable and, in effect, a group of two or more predictor variables.

Question 7

Partial correlation coefficients measure

Answer 7

The correlation between the dependent variable and each of the individual predictors, but, again, holding constant all other predictors in the model.

Question 8

Partial correlations are useful when we want to

Answer 8

Examine the intrinsic association between two variables in complex multivariate situations.

Question 9

Number of ‘controlled’ variables determines

Answer 9

The order of correlation. Simple correlations are zero-order. First-order partial correlations have only one controlled variable, but can be derived from the various zero-order correlations between each of the variables in the data set.

Question 10

Multicollinearity

Answer 10

Refers to the situation where correlation exists between several predictor variables. When two predictors are strongly correlated their respective zero-order correlations with dependent variable may often suggest similarly strong degrees of association to exist.

Question 11

Difficulty of multicollinearity comes from

Answer 11

The fact that in multiple regression we might be tempted to employ two such variables, both of which appear to have a strong correlation with the dependent item, only to find that one of them emerges as having a very weak partial influence, and its seemingly strong zero-order association results only from its correlation with the other.

Question 12

Partial Regression Coefficients

Answer 12

A measure of the impact of a predictor on the dependent variable when other predictors are preesent but held constant. b_1,b_2…b_n are scale dependent.

In common with their simple counterparts, are scale dependent, and have magnitudes that are partly determined by the units in which Xi and Y are measured.

Question 13

Beta Weights

Answer 13

Standardise coefficients. Partial regression coefficients don’t really tell you anything about the relative importance of predictors of Y. Whereas, the beta are much more comparable.

Question 14

Explained Variance

Answer 14

Deviation of predicted values of Y from the mean of Y.

Question 15

Unexplained variance

Answer 15

Deviation of actual values of Y from predicted value of Y.

Question 16

Assessing multicollinearity (two methods)

Answer 16

Tolerance scores - unique variance of each independent variable. 0.34 means 34% of the variance is not accounted for by other predictors. Tolerance of 0.20 or below is problematic.

Pairwise correlation of independent variables.

Variance inflation factor (vif score) - score of 1 = absence of multicollinearity, 3 = rejection threshold in SPSS, value greater than 5 = presence of multicollinearity, value of 10 and above = Complete multicollinearity.

Question 17

Ways to address multicollinearity

Answer 17

Remove one or more of the correlated variables from the regression model or where there is a logical relationship between two x variables, create an interaction term, or, if variables are related due to underlying factors controlling Y, they may be reduced using factor or principal component analysis.

Question 18

The F-test

Answer 18

Comparing regression models.

Question 19

Strategies for undertaking multiple regression

Answer 19

Do not employ scattergun approach. Select variables based on theory and previous findings. Careful analysis of the charcater of relationships. Don’t rely on a single metric.

Question 20

Parsimony

Answer 20

The simplest model explanation/interpretation should be sought.

Question 21

Hierarchical regression

Answer 21

The practice of building successive models, each one adding more predictors. Researchers decide on order to list predictors. Order based on theoretical considerations.

Question 22

Simultaneous regression

Answer 22

All independent variables are analysed simultaneously on an equal footing. An appropriate course when there is no theoretical consideration underpinning the importance of variables.

Question 23

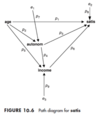
Path Analysis

Answer 23

Examines the relationships between 3 or more variables. Provides quantitative estimates of the causal connections between sets of variables.

Model moves from left to right - indicating causal priority to the left.

Arrows outside nexus - unexplained variances

Numbers (p) are beta values.