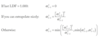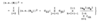Section A: Estimating Parameters Flashcards
(80 cards)
Clark: What are the primary objectives of Clark’s paper? What are the two key elements from those objectives?
Objective 1:
- to provide a tool that describes the loss emergence
Objective 2:
- to provide a way of estimating a range of possible outcomes around the expected reserve
The 2 key elements:
- the expected amount of loss to emerge in some time period
- the distribution of actual emergence around the expected value (stochastic reserving)
Clark: Expected Loss Emergence
Weibull
- generally provide small tail factor than Loglogistic
- if given Wiebull on the exam, you shouldn’t need to truncate the data or need a tail factor
- Loglogistic you will require to truncate as it has a heavier tail
- note that ‘x’ is cumulative time average so from accident year to valuation point and then half of the last valuation point (so 120 months then ‘x’ is 114)
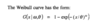
Clark: Expected Loss Emergence
Loglogistic (Inverse Power)
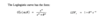
Clark: What are the advantages of using parameterized curves to determine the expected emergence pattern?
- simple method as we only need to estimate 2 parameters
- can use triangles with partial periods
- indicated pattern is a smooth pattern and will not have random movement seen in the historical age-to-age factors
Clark: What is the benefit of using the Loglogistic and the Weibull curves to derive the reporting pattern?
- Smoothly move from 0% to 100%
- these two models will work when some actual points show decreasing losses; however, if there is real expected negative development then a different model should be used
- e.g. significant salvage recoveries you may see on physical damage
- these two models will work when some actual points show decreasing losses; however, if there is real expected negative development then a different model should be used
- Closely match empirical data
- First and second derivatives are calculable
- Can be used on partial periods
Clark: Estimating Ultimate Losses
LDF Method
µAY;x,y = ULTAY * [G(y|w,ø) - G(x|w,ø)]
Clark: Estimating Ultimate Losses
Cape Cod Method
Explain why CC is better than LDF method?
µAY;x,y = PremiumAY * ELR * [G(y|w,ø) - G(x|w,ø)]
- Cape Cod method has a smaller parameter variance
- Process variance can be higher or lower than the LDF method
- In general, Cape Cod is preferred to LDF method since:
- LDF method is overparameterized due to less data points as we are using annual triangle
- CC has lower total variance driven by
- reduced number of parameters
- using more information (premium/exposure base)
Clark: The distribution of actual loss emergence process variance is given by the following:
σ2 = ?
- assume that c follows an over-dispersed Poisson distribution with scaling factor σ2
- this is the same thing as the Chi-Square error term which is then scaled by n-p

Clark: What are the advantages of using the over-dispersed Poisson distribution?
Advantages
- scaling factors allow us to match the first and second moments of any distribution which offers a high degree of flexibility
- MLE produces the LDF and CC estimates of ultimate losses so can be presented in format familiar to reserving actuaries
Clark: Should we be concerned about estimating ultimate reserves using a discrete (Poisson) distribution?
- the scale factor, σ2, is genearlly small compared to the mean so little precision is lost
- allows for probability mass function (p.m.f.) at zero which mean there can be cases where no change in loss is seen
Clark: What is the liklihood estimator of the Poisson distribution?
MLE = Σci * ln(ui) - ui
Clark: What is the formula for the Cape Cod Ulitmate?
ELR = ?
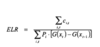
Clark: What is the formula for the LDF ULTi?
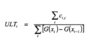
Clark: What is an advantage of the maximum loglikelihood function?
- it works in the presence of negative or zero incremental losses
- since its based on expected incremental development and not actual
Clark: What is the total variance of the reserves?
Total Variance = ?
- Total variance is the sum of the process variance and the parameter variance
- Due to the complexity of the parameter variance, it should be given to us on the exam
Process Variance of R = σ2ΣµAY;x,y
Clark: What are the key assumptions of the stochastic reserving model?
1. Incremental losses are independent and iid
In context of reserving:
- independent means one period does not affect surrounding period
- could see positive correlation if all periods are equally impacted by change in loss inflation
- could see negative correlation if large settlement in one period replaces a stream of payments in later periods
- identically distributed assumes the emergence pattern is the same for all accident years (over simplified assumption as mix of business changes would impact this)
2. The variance/mean scale parameter, σ2, is fixed and known
- simplifies the calculations
3. Variance estimates are based on an approximation to the Rao-Cramer lower bound.
- do not know the true parameters so this is an approx.
Clark: Set up the table needed to solve for the reserves.
LDF Method

Clark: Set up the table needed to solve for the reserves.
Cape Cod Method
- MAKE sure to calculate the ELR PRIOR to truncation!
- have to do it this way as per Clark to get the right answer
- parameters will be different since on-level premium is needed so lag factors differ from LDF method
- add a column for OLP

Clark: How do you determine the process variance of the total reserve?
Just multiply the reserve by the scale factor, σ2
Clark:
rAY;x,y =
What are you looking for when examining the residual plots?
- We want the residuals to be randomly scattered around the zero line
- Can plot the residuals against a number of things to test the model assumptions such as:
- Increment Age (i.e. AY age)
- Expected loss increment - good for testing the variance/mean ratio is constant
- Accident Year
- Calendar Year - to test diagonal effects

Clark: Once the MLE calculations have been completed, there are other uses for the statistics besides the variance of the overall reserve. What are 3 uses?
1. Variance of the Prospective Loss
- Must use Cape Cod for this as we already have the MLE of the ELR
- Can use this to estimate the expected loss if we already have future premium (from budget)
2. Calendar Year Development
- This is AvE as we can estimate the development for the next CY beyond the latest diagonal.
- Good reason for this is that the 12-month development is testable within a short timeframe. One year later we can compare it to actual development and see if its in the forecast range.
3. Variability in the Discounted Reserves
- lower CV as the tail has the greatest process variance but it also gets the deepest discount
Clark: Variance of the Discounted Reserves
Rd = ?
Var(Rd) = ?

Clark: How do you calculate the estimated reserves for partial periods on an AY basis?
- must multiply the Expos(t) by G(x)
- e.g. if its September then the current year will have Expos(t) = 0.75 and G(4.5) and then you would multiply this together to get the adjusted G(x)
- for years not in the first 12 months, the Expos(t) factor is 1
Mack (1994): Mack Chain Ladder Assumption 1
Mack Assumption 1
Expected losses in the next development period are proportional to losses-to-date
E[Ci,k+1 | Ci,1,…,Ci,k] = Ci,k * LDF
- The chain ladder method uses the same LDF for each accident year (volume weighted average)
- Uses most recent losses-to-date to project losses, ignoring losses as of earlier develoment periods