Roots, Exponents, Decimals, Ratios & Percents

Question 1

Square Root of 2

Answer 1

≈ 1.4

Question 2

Square Root of 3

Answer 2

≈ 1.7

Question 3

Square Root of 5

Answer 3

≈ 2.25

Question 4

Square Root of 6

Answer 4

≈ 2.4

Question 5

Square Root of 7

Answer 5

≈ 2.6

Question 6

Square Root of 8

Answer 6

≈ 2.8

Question 7

1/x^a

Answer 7

= x^-a

Question 8

1/x^-a

Answer 8

= x^a

Question 9

x²< x < x^1/2

if…

Answer 9

0 < x < 1

“x is a proper fraction”

Question 10

If the base is < -1

&

base^{(+)even int.}

** -2² **

The resulting # is….

Answer 10

> the base.

** (+)4

Question 11

If the base is < -1

&

base^{(+)odd int.}

** -2³**

The resulting # is…

Answer 11

< the base

** -8 **

Question 12

If the base is (+) proper fraction

&

base^{(+) evenint.}

** 1/4²**

The result is…

Answer 12

< the base

** 1/16 **

Question 13

If the base is (-) proper fraction

&

base^{(+) <strong><em>odd</em></strong> int.}

** (-1/3)³**

The result is…

Answer 13

> the base

** ( -1/27) > (-1/3) **

Question 14

If the base > 1

&

base^{(+) <b><i>proper fraction</i></b>}

** (16)^1/2**

The result is…

Answer 14

< the base

** 4 < 16 **

Question 15

If the base is (+) proper fraction

&

base^{(+) <b><i>proper fraction</i></b>}

** (1/4)^1/2**

The result is…

Answer 15

> the base

** ( 1/2 > (-1/4) **

Question 16

Square root of perfect square scaled to a large number with an EVEN # of “0’s”

=

Answer 16

a # with exactly half the # of zeros to the right of the final non-zero digit as the perfect square.

= 9,000

Question 17

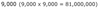
Cubed root of perfect cube scaled to a large number

=

Answer 17

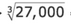
has 1/3rd the number of zeroes to the right of the final nonxero digit as the perfect cube in question

Question 18

Squaring Decimals w/ Zeroes

(0.00005)² = ?

Answer 18

Double the amount of decimal places NOT just the zeroes.

• So…*
  (0. 00005)² has a total of 5 decimals places to the right of decimal point
• Therefore…*

The result should have 2x5 (10) decimals places to the right of the decimal point. THIS INCLUDES THE ACTUAL SQUARED #

ANSWER =

.0000000025

(10 total decimal places to the right of the decimal point)

Question 19

Xⁿ+ Xⁿ=

Answer 19

Xⁿ⁺¹

Remember that there has to be a pair of numbers of the same base raised to the same exponent.

Question 20

“Decrease of 20%” … “Increase of 25%”

Answer 20

Back to original #.

No % change.

Question 21

1/6

Answer 21

16.67%

(16%)

Question 22

5/6

Answer 22

=

0.83

or

83%

Question 23

1/100

Answer 23

=

0.01

or

1%

Question 24

3/8

Answer 24

=

.375

or

37.5%

Question 25

1/8

Answer 25

=

.125

or

12.5%

Question 26

7/8

Answer 26

=

.875

or

87.5%

Question 27

5/8

(hint: 1/2 + 1/8)

Answer 27

=

.50 + .125 ► .625

or

50% + 12.5% ► 62.5%

Question 28

“X varies inversely with Y”

Answer 28

X = k/Y

Question 29

“X varies directly with Y”

Answer 29

X = kY

Question 30

• If* x:y and z:x….
• then* what is x:y:z?

Answer 30

find the LCM of the common variable (x) to produce a 3-part ratio

(generally works)

Question 31

Percent Increase

Answer 31

Final Value = Initial Value ( 1 + “percent greater than”/100)

Question 32

Percent Less Than

Answer 32

Final Value = Initial Value (1 - “percent less than”/100)

Question 33

Percent Change

Answer 33

[(Final Value - Initital Value)/Initital Value} x 100

Question 34

Profit

Answer 34

= (Purchase Price) x (Purchase Percentage)

Question 35

Selling Price

Answer 35

= (Profit) + (Purchase Price)

Question 36

11²

Answer 36

= 121

Question 37

13²

Answer 37

= 169

Question 38

14²

Answer 38

= 196

Question 39

15²

Answer 39

= 225

Question 40

4³

Answer 40

= 64

Question 41

5³

Answer 41

= 125

Question 42

6³

Answer 42

= 216

Question 43

7³

Answer 43

= 343

Question 44

8³

Answer 44

= 512

Question 45

9³

Answer 45

= 729

Question 46

10³

Answer 46

= 1000

Question 47

0⁰

Answer 47

= 1 or undefined

Question 48

2⁸

Answer 48

= 256

Question 49

2⁴

Answer 49

= 16

Question 50

2⁵

Answer 50

= 32

Question 51

2⁶

Answer 51

= 64

Question 52

2⁷

Answer 52

= 128

Question 53

3³

Answer 53

= 27

Question 54

3⁴

Answer 54

= 81

Question 55

4³

Answer 55

= 64

Question 56

4⁴

Answer 56

= 256