Number Props Flashcards
- Only # = to it’s opposite
- Multiple of all #’s
- Not a factor of any # except itself
- An even number
- Neither negative nor positive
0 (Properties of Zero)
How to find “trailing zeroes” or number of 10s in a large #
Find the number of 2’s and 5’s you have. Whichever number is represented the least amount of times is the number of trailing zeros
odd #/odd# =
odd
even/odd =
even
odd x odd =
or
odd x odd x odd =
odd
odd - even =
or
even - odd =
odd
odd + even =
or
even + odd =
odd
even - even =
even
odd - odd =
even
odd + odd =
even
Odd Integers
Can be represented by (2n+1) or (2n-1)
where “n” is odd
Even Integers
Can be represented by (2n) where “n” is an interger Has an even units digit Divisible by 2
Prime #’s
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101
Total # of factors for a given integer
Step 1: Determine prime factorization for integer
Step 2: Add 1 to the value of each exponent
Step 3: Multiply those values (i.e. “new exponents”), the product is your answer.
The # of unique prime factors does not change if…
the number in question is raised to any other positive integer power
LCM (Definition)
the smallest positive integer into which all of the numbers in question will divide into
or
the smallest positive multiple of all numbers in the set
Finding the LCM of a set of positive integers
Step 1: Prime factorize all integers in set.
Step 2: Of any repeated prime factors, only take the ones with the largest exponent.
Step 3: Take any non repeated prime factors.
Step 4: Multiply numbers from Step 2 & 3. ** If numbers in set do not share any prime factors, then multiply all numbers in the set.
Numbers divisible by 4
Last two digits of the number are divisible by 4 Any number that ends in “00” All multiples of 100
Numbers divisible by 8
Divide the last 3 digits of even number to determine Any number that ends in 000 All multiples of 1000
Numbers divisible by 11
The (sum of the odd-numbered digits) - (sum of the even-numbered digits) = number divisible by 11
Numbers divisible by 12
Number is divisible by BOTH 3 & 4
Finding the GCF
Step 1: Prime factorize each int. in the set. Put prime factors in exponent form
Step 2: Identify repeated prime factors
Step 3: Of the repeated prime factors, take only the one with the smallest exponent. Discard non-repeated prime factors
Step 4: Multiply numbers found in Step 3 ** If the set has no prime factors in common, the answer is 1.
Formula for division w/ a remainder
X = YQ + R
or
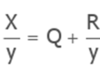
“4” Units Digit Pattern
4-6-4-6
“3” Units Digit Pattern
3-9-7-1
“5” & “6”
Units Digit Pattern
All powers of 5 and 6 end in 5 & 6
“7” Units Digit Pattern
7-9-3-1
“8” Units Digit Pattern
8-4-2-6
“9” Units Digit Pattern
9-1-9-1
“2” Units Digit Pattern
2-4-8-6
If
|x+y| = |x| + |y|
and x & y are both non-zero integers
then…
x & y have the same sign
If
|x| - |y| = |x-y|
then…
x & y have the same sign
&
|x| > |y|
If x2 > b
and b > 0
then….
x > b1/2
&
x 1/2
- thus*
- b1/2 > x > b1/2
Note: If it’s a > sign the rule works out the same way
Determining numerator & denominator from a word problem
look for “is” and “of”
translate as
is/of
or (a/b) x 100
(x4 - y4)
=
(x2 - y2)(x2 + y2)
Notating Even Consecutive Integers
2n, 2n + 2, 2n + 4, 2n + 6, …
Notating Odd Consecutive Integers
2n + 1, 2n + 3, 2n + 5, 2n + 7, …
(a2 - b2)
=
(a+b) (a-b)
Square of a Sum
(a+b)2
=
a2 + 2ab + b2
Square of a Difference
(a-b)2
=
a2 - 2ab + b2
GCF for Consecutive Integers
n & n+1
No shared factors so the GCF
=
1
(LCM of x & y) x (GCF of x & y)
=
Product of x & y
(x)(y)
Finding the Unique Primes of Two #’s
(Shortcut)
Find the LCM of both numbers
Is this number a perfect square?
If the prime factorization of the number yields
primesraised to even expoents
then it is a perfect square.
Terminating vs. Non-terminating Decimals
If the denominator of the fraction in question has a prime fatorization of only 2’s, 5’s or both it will terminate!
Any other primes = non-terminating decimal
Division Properties of Factorials
n! must be…
- Divisible by all integers from 1 to n inclusive
- Divisible by any combination of integers from 1 to n inclusive
For positive integers x & y
Is y a factor of x?
Yes, if x/y is an integer.
Product of any 3 consecutive integers
(n)(n+1)(n+2)
or
(n-1)(n)(n+1)
is always divisible by 6
Product of any 3 EVEN consecutive integers
(n)(n+2)(n+4)
or
(2n)(2n+2)(2n+4)
or
(n-2)(n)(n+2)
is always divisible by 6
The absolute value of the additon of two numbers
|a + b|
will…
Always be less or equal to the absolute value of
a plus the absolute value of b
|a + b| < |a| + |b|
The absolute value of the subtraction of two variables
|x - y|
is…
greater than or equal to the subtraction of the
absolute value of the 1st variable minus the absolute value of the 2nd variable
|x - y| > |x| - |y|
If the absolute value of an expression is equal to a negative number
|x + 1| = -4
Wait…what?!1/
The absolute value of an expressions can never equal a negative number!
Never
EVER!
