Review of Basic Concepts

Question 1

Central Limit Theorem

Answer 1

For non-normal data, the distribution of the sample means has an approximately normal distribution, no matter what the distribution of the original data looks like, as long as the sample size is large enough (n >= 30) AND all the samples have the same size.

Question 2

Sampling Distribution of the Sample Mean is also known as…

Answer 2

The probability distribution of the sample mean.

Question 3

Sampling Distribution of the Sample Mean

Answer 3

Repeated random samples of a given size (n), taken from a population of values, result in the mean of all sample means (x-bars) to equal population mean (μ).

Question 4

With the Casio calculator, answer the following:

The weight of adults is normally distributed with a mean (µ) = 175 lbs and standard deviation (σ) = 20 lbs. Supposed a random sample of size (n) = 36 adults is selected.

What is the probability that the sample mean is between 160 lbs and 180 lbs?

Answer 4

Because we’re trying to determine the sample mean probability, we can’t use the population standard distribution for the inputs. We need to make sure we use the SAMPLE standard deviation, which is denoted with the following formula:

σ/√n

STAT
DIST
NORM
Ncd

Inputs

• *Data:** Variable
• *Lower:** 160
• *Upper:** 180
• *σ:** 20/√​36 ♦
• *µ:** 175

Outputs

• *P =** 0.9331894
• *Z:Low =** -4.5
• *Z:Up =** 1.5

Question 5

With the Casio calculator, answer the following:

The final exam mark for a class is normally distributed with a mean (µ) of 68 and standard deviation (σ) of 14. What is the probability that a randomly selected student’s mark is greater than 60?

Answer 5

STAT
DIST
NORM
Ncd

Inputs

• *Data:** Variable
• *Lower:** 60
• *Upper:** 1_E99
• *σ:** 14
• *µ:** 68

Outputs

• *P =** 0.71614541
• *Z:Low =** -0.5714285
• *Z:Up =** 7.1429_E+97

Question 6

With the Casio calculator, answer the following:

The body weight for adults is normally distributed, with a mean of 65 kg and standard deviation of 10 kg. A student’s body weight is 70 kg. What is the z-score for this student’s body weight?

Answer 6

STAT
DIST
NORM
Ncd

Inputs

• *Data:** Variable
• *Lower:** 70
• *Upper:** 1_E99
• *σ:** 10
• *µ:** 65

Outputs

• *P =** 0.30853753
• *Z:Low =** 0.5
• *Z:Up =** 1_E+98

Question 7

Given the data: 229, 255, 280, 203, 229, estimate the population mean using 95% confidence interval.

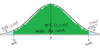
Hint: Take a look at the distribution image to determine the first steps.
Hint: Note how many data are provided in the sample.

Answer 7

1. Determine the degree of freedom:

n - 1 = 5 - 1 = 4

2. Determine the mean (x̄ = 239.2) and standard deviation (s = 29.29505078) of the sample data set.
3. Using the confidence level, we need to determine what is the area under the curve. This can be determined using the following formula:

(1 + Confidence Level) / 2
(1 + 0.95) / 2
1.95 / 2
0.975

3. Using the t table we want to determine the t_STAT for a cumulative probability of 0.975 and with df=4.

t_STAT = 2.776

Note: We are using the t_STAT due to the number of items in our sample (n) being < 30.

3. Once we know the t_STAT pertaining to the population based on the sample we have, we can plug the values into the formula as shown below:

x̄ ± t_{STAT ^x} (s/√n)

239. 2 ± 2.776 _^x (29.29505078/√5)
240. 2 ± 2.776 _^x (13.10114499)
241. 2 ± 36.36877849

Result: 202.8312215 < µ < 275.5687785

Question 8

A report contains the attention span data for 50 randomly selected twins from the underlying population. What are the steps to determine the 99% confidence interval for a population mean using the Z_STAT as an approximation to the sampling distribution if: sample mean (x̄) = 20.85 and sample standard deviation (s) = 13.41?

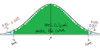
Hint: Take a look at the distribution image to determine the first steps.

Answer 8

1.Using the confidence level, we need to determine what is the area under the curve. This can be determined using the following formula:

(1 + Confidence Level) / 2
(1 + 0.99) / 2
1.99 / 2
0.995

The value of 0.995 includes the confidence level + the left most area under the curve.

2. Using the Z table we want to determine the Z_STAT for an area of 0.995.

Note: on most Z tables, there is no value for 0.995! The values closest are 0.9949 and 0.9951. The Z values for these is 2.57 and 2.58 respectively.

Using a Z table calculator however, you can obtain a more precise Z value of 2.575829.

3. Once we know the ZSTAT pertaining to the population based on the sample we have, we can plug the values into the formula as shown below (a more clear example is attached as an image):

x̄ ± Z_STAT x (s/√n)

20. 85 ± 2.575829 x (13.41/√50) 20.85 ± 2.575829 x (1.896460387)
21. 85 ± 4.884957663

Result: 15.96504234 < µ < 25.73495766

Question 9

When do we need to use the Z critical value?

Question 10

How do we use the p-value of a hypothesis test to make a statistical decision?

Question 11

What is a critical value?

Answer 11

A critical value, is a value used in hypothesis testing. It is a point on the test distribution that is compared to the test statistic to determine whether to reject the null hypothesis.

Question 12

What are the two methods that can be used to determine whether there is enough evidence from the sample to reject H₀ or fail to reject H₀?

Answer 12

Method 1: Compare the p-value with a specified value of α, where α is the probability of rejecting H₀ when H₀ is true.

Method 2: Compare the calculated value of the test statistic with the critical value

Question 13

True or False

The rejection region for a hypothesis test is determined by the alternative hypothesis.

Answer 13

True.

The alternative hypothesis of µ > µ₀ indicates an upper tail test.

Similarly, the alternative hypothesis of µ 0 indicated a lower tail test.

Question 14

Based on the p-value in the image, should we reject or not reject the null hypothesis? Why?

Answer 14

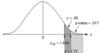
We would reject the null in this case, because the p-value is less than α.

Question 15

To which value is the p-value compared when making conclusions in significance testing?

Answer 15

The p-value is compared to the significance level ( α ) of a hypothesis test.

Question 16

If the p-value is __________ than or equal to the significance level we chose, then we fail to reject the null hypothesis H_0. This does not mean we accept H₀.

Answer 16

greater

Question 17

If the p-value is __________ than the significance level we chose, then we reject the null hypothesis H₀ in favour of the alternative hypothesis H_a.

Answer 17

lower

Question 18

When p-value >= α,
reject / fail to reject H₀.

Answer 18

Fail to Reject

Question 19

When p-value reject / fail to reject H₀.

Answer 19

Reject

Question 20

Sample question:

A certain bag of fertilizer advertises that it contains7.25 kg, but the amounts these bags actually contain is normally distributed with a mean of 7.4 kg and a standard deviation of 0.15 kg.

The company installed new filling machines, and they wanted to perform a test to see if the mean amount in these bags had changed. Their hypotheses were H₀: µ = 7.4 kg vs. Ha: µ ≠ 7.4 kg (where µ is the true mean weight of these bags filled by the new machines).

They took a random sample of 50 bags and observed a sample mean and standard deviation of x̄ = 7.36 kg and s_x = 0.12 kg . They calculated that these results had a P-value of approximately 0.02.

What conclusion should be made using a significance level α=0.05?

a. Fail to reject H₀
b. Reject H₀ and accept H_a
c. Accept H₀

Answer 20

Reject H₀ and accept H_a.

Since the p-value of 0.02 is less than α = 0.05, we should reject H₀ and accept H_a.

Question 21

Sample question:

Alessandra designed an experiment where subjects tasted water from four different cups and attempted to identify which cup contained bottled water. Each subject was given three cups that contained regular tap water and one cup that contained bottled water (the order was randomized). She wanted to test if the subjects could do better than simply guessing when identifying the bottled water.

Her hypotheses were H₀: p = 0.25 vs H_a: p > 0.25 (where p is the true likelihood of these subjects identifying the bottled water).

The experiment showed that 20 of the 60 subjects correctly identified the bottle water. Alessandra calculated that the statistic p̂ = 20/60 = 0.333 had an associated P-value of approximately 0.068.

What conclusion should be made using a significance level α=0.05?

a. Fail to reject H₀
b. Reject H₀ and accept H_a
c. Accept H₀

Answer 21

Fail to reject H₀.

Since the p-value of 0.068 is greater than α = 0.05, we should fail to reject H₀.

Question 22

What statistical test should be used when comparing two population variances?

Answer 22

F test

Question 23

What is the ANOVA test used to determine?

Answer 23

This test is used to run hypothesis testing on more than 2 population means to see if any of the population means differs from the others.

Question 24

MSE

What test uses this abbreviation and what does this abbreviation represent. Explain.

Answer 24

MSE is an abbreviation used with the ANOVA test

It represents the mean square error across all groups and can be calculated as follows:

MSE = SSE/(n-k); Where n = grand mean for all groups and k is the number of groups being tested.

Question 25

MSA

What test uses this abbreviation and what does this abbreviation represent. Explain.

Answer 25

MSA is an abbreviation used with the ANOVA test

It represents the mean square among groups and can be calculated as follows:

MSA = SSA/(k-1); Where k is the number of groups being tested.

Question 26

SSE

What test uses this abbreviation and what does this abbreviation represent. Explain.

Answer 26

SSE is an abbreviation used with the ANOVA test

It represents the sum of squares within groups.

Question 27

SSA

What test uses this abbreviation and what does this abbreviation represent. Explain.

Answer 27

SSA is an abbreviation used with the ANOVA test

It represents the sum of squares among groups.

Question 28

How is the test statistic for ANOVA calculated? Which test is supposed to be used to do so?

Answer 28

The test statistic is calculated with the following equation: MSA/MSE.

This equation provides results for the F test statistic to test the ANOVA hypothesis.