ANOVA

Question 1

What is the regression error sum of squares (SSE)?

Answer 1

SSE (Error Sum of squares) is variation due to factors other than the relationship between X and Y

Question 2

What is the regression sum of squares (SSR)?

Answer 2

SSR (Sum of squares) is a variation that is explained by the relationship between X and Y

Question 3

How is the SST value calculated?

Answer 3

SST is the total sum of squares. It is deermined by adding SSR and SSE to get a complete measure of variation of the Y_i values around their mean (Ȳ).

Question 4

What does the correlation coefficient (r) measure?

Answer 4

The correlation coefficient measures the strength of the relationship between X and Y.

Question 5

What is the coefficient of determination(r²)?

Answer 5

The coefficient of determination is the regression sum of squares, divided by the total sum of squares.

r² = SSR/SST

Question 6

What is the difference between:

coefficient of determination and correlation coefficient?

Answer 6

The correlation coefficient (r) is multiplied by itself to get the coefficient of determination (r²).

The coefficient of determination (r²)demonstrates a percentage of variation in y, which is explained by all the x variables in the model. This value is always between 0 and 1.

The coefficient of correlation (r) is the degree of relationship between two variables, i.e. x and y. It can fall between -1 and 1.

Question 7

What is another term for the concept of “Residual”?

Answer 7

Estimated error value.

Question 8

What is the equation to calculate residuals (estimated error value) for any point in a regression model?

Answer 8

e_i = Y_i - Ŷ_i

Where Y_i is the observed value and Ŷ_i is the predicted value.

Question 9

What table is displayed in the image? What is it for?

Answer 9

ANOVA table.

It is used to summarize regression terms applicable to models being evaluated. Especially to determine the F test statistic and p-value for hypothesis testing against a regression model.

Question 10

For a straight line probabilistic model, there are 6 possible relationship types. WHat are they?

(Hint: PL, NL, PC, NC, UC, NA)

Answer 10

Positive linear

Negative linear

Positive Curvilinear

Negative curvilinear

U-shaped Curvilinear

No relationship

Question 11

What part of the simple linear regression model is the deterministic component?

Answer 11

Y=β₀+β₁X+ε is the simple linear regression model.

E(y) =β₀+β₁X is the deterministic component of the regression model.

Question 12

What is the model equation for a simple linear regression model?

Answer 12

Y=β₀+β₁X+ε

Where Y = dependent variable (aka response variable)

β₀ = y-intercept for the population

β₁ = slope for the population

X = independent variable (aka predictor of Y)

ε = random error component

Reminder: without the ε component, the equation

E(y) =β₀+β₁X is the deterministic component of the regression model.

Question 13

What are three measures of variation to observe when working with linear regression models?

Answer 13

SSR (regression sum of squares)

SSE (error sum of squares)

SST (total sum of squares)

Question 14

How do we calculate the SST (total sum of squares)?

This is the total sum of squares.

Answer 14

∑(Yi - Ȳ)²

This reads as the sum of the difference between the observed Y and the average of Y, squared.

Question 15

How do we calculate the SSE (error sum of squares)?

This is the unexplained variation or error sum of squares.

Answer 15

∑(Yi - Ŷi)²

This reads as the sum of the difference between the observed Y and the predictedY, squared.

Question 16

How do we calculate the SSR (regression sum of squares)?

This is the explained variation or regression sum of squares.

Answer 16

∑(Ŷi - Ȳ)²

This reads as the sum of the difference between the predicted Y and the average of Y, squared.

Question 17

If a coefficient of determination (r²) is found to be 0.817, what does this mean?

Answer 17

It means that 81.7% of changes in Y can be explained by X.

R² is usually explained in terms of percentage.

Question 18

What is the standard error of the estimate (S_xy) used to determine?

Answer 18

The standard error of the estimate is used to measure the variability of the observed Y from the predicted Y. This also can be described as the measure of variation of an observation made around the computed regression line.

It is similar to a standard deviation (which measures the variation in the set of data from the mean).

Question 19

How is the standard error of the estimate calculated?

Answer 19

Sxy = √SSE/(n-2)

Question 20

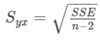
Which of the outputs in the ANOVA table are used to calculate the standard error of the estimate (S_xy)?

Answer 20

The standard error of the estimate is calculated using the SSE.

S_xy = √SSE/(n-2)

Question 21

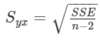
What coefficient measures the strength between Y and X?

Answer 21

Regression coefficient

Question 22

What measures variation due to factors other than the relationship between X and Y?

Answer 22

Error sum of squares SSE

Question 23

What measures how much change in Y can be explained by X?

Answer 23

Coefficient of determination