Regression; Lec 8; Lab 4 Flashcards
What is a coefficient?
A factor that makes up a particular property
What does a significant r mean?
That the regression coefficient is also significant
Which variable goes on X axis and which goes on Y axis?
Variable which ‘varies’ (IV) on the X-axis Variable measured (DV) on the y-axis
If you want to predict university score from SAT scores - which is predictor variable and which is criterion variable?
SAT score is predictor variable
University score is criterion variable
What is a negative correlation?
As one variable increases so the other decreases
What does it mean when variables are said to covary?
That they have either a positive or negative correlation to one another
What is the predictor variable?
Independent variable - used to predict an outcome (variable that varies)
What are three things that are important to remember in regression?
- Any set of data can have a regression line plotted
- The significance of the correlation or regression tells us whether a real relationship exists
- The correlation or the standard error of estimate tells us how accurate the regression equation is
How should
rxy = cov(x,y)/SxSy
Where
Covxy = Σ(X - Xbar)(Y - Ybar)/N-1
be interpreted?
- It is an indication of how closely the data points lie along the line of best fit (the regression line)
- Like all stats requires a p value to determine whether the relationship is due to chance or is the product of a real relationship
what is r2 =
The proportion of the variance in the DV that is predictable from the IV.
Regression produces eight different analyses:
- Descriptive statistics,
- correlations,
- variables entered/removed,
- Model summary,
- ANOVA,
- Coefficients,
- Casewise diagnostics,
- Residual Statistics
First we look at ‘casewise diagnostics’, which should we look at second? Why?
Model summary
This is related to the correlation
r is the Pearsonn correlation restated
r2 is the coefficient of determination (a measure of relative variability) and indicates how much of the variation in the DV can be explained by variation in the IV
‘Std. Error of the Estimate’ is the std. error of prediction for all the values - this gives up a direct measure of the potential of our predictions using the regression equation. You compare this score to the SD of the criterion variable to get an indication of how useful the regression is (if the score in the regression is lower than that of the criterion variable score than it is useful)
What is this the formula for?
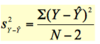
Note: in this instance the denominator = N-2 because we are imagining 2 values involved in the prediction
Residual/error variance
Regression produces eight different analyses:
- Descriptive statistics,
- correlations,
- variables entered/removed,
- Model summary,
- ANOVA,
- Coefficients,
- Casewise diagnostics,
- Residual Statistics
First we look at ‘casewise diagnostics’, then we look at ‘Model summary’, what should we look at third? Why?
Coefficients (factor that makes up a particular property)
- Column ‘B’, the value idenitified as constant is the intercept (a in regression equation)
- Slope/gradiant of the line = identified by name given to predictor variable (b in regression equation)
H0 rho =
0
where rho is the population correlation coefficient
r2 can give us % predictable variance. Using the smoking and CHD example, where r2 = .7232 = .508, explain.
r = .713
r2 = .7232 = .508
Approximately 50% in variability of incidence of CHD mortality is associated with variability in smoking - NOTE: you cannot infer a cause and effect relationship
This is the formula for the regression of the line.
How do you calculate b?
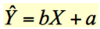
SX2 = variability of X
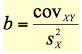
What is the standard error of prediction?
Standard dev. of all predicted values minus the recorded value.
How do we know if our prediction is better than just using the mean?
Total SS - residual SS
What is the criterion variable?
Dependent variable (variable measured)
What can badly affect Pearson’s r?
- Data with outliers
- Data that is not linear (e.g. curvilinear - a smooth curve of any shape)
Covxy = ?
Covxy = Σ(X - Xbar)(Y - Ybar)/N-1
There are two possible ways to predict - what are they?
- Basic = difference from mean scores (average Y)
- Total sums of square
- Regression = difference from the regression line (difference from Yhat)
If you want to predict the incidence of CHD in population based on incidence of smoking - which is the predictor variable? Which is the criterion variable?
- Predictor variable X (IV) = average number of cigarettes smoked per head of population
- Criterion variable Y (DV) = incidence of CHD
How do you remove a data point from analysis?
Data –> Select cases –> ‘Select Cases’ dialogue box –> ‘If condition is satisfied’ –> ‘If…’ –> move variable you want to exclude to box and then put ~ (tilda - should not equal) and then type value of outlier you want to remove (e.g. 12.45) –> continue –> OK
Then you must re-run the analysis you wanted to run.
What are each of the values for the regression equation:
Predicted score = b x (predictor score) + a
Predicted score = (Slope/gradiant of the line from coefficients output) x (predictor score) + (Coefficients output column ‘B’, the value idenitified as constant is the intercept)
What is the linear regression equation?
Yhat = predicted value of Y
X = smoking incidence in a country
b = slope of line - change in predicted Y due to one unit change in X
a = the intercept - the value of Yhat when X is at 0
There are 4 columns in the casewise diagnostics output:
- Std. Residual
- Case number
- Predicted value
- Residual
What do each of them mean?
- Std. residual = identifies how many stardard errors of prediction the selected data point is away from the regression line
- Case number = Participant number
- Predicted value = What SPSS (regression) predicted the value would be
- Residual = The gap between the predicted score and the actual score
How would you summarise what correlation summarises?
Correlation quanitifies the potential linear relationship between two variables; the supposition of linearity must be confirmed by inspection of the scatterplot
What
How would you run a regression analysis in SPSS?
Analyze –> Regression –> Linear –> Move predictor variable (IV) to ‘Independents’ box –> Move criterion variable (DV) to ‘Dependents’ box –> Statistics –> Descriptives –> Casewise diagnostics –> Continue –> OK
Regression produces eight different analyses:
- Descriptive statistics,
- correlations,
- variables entered/removed,
- Model summary,
- ANOVA,
- Coefficients,
- Casewise diagnostics,
- Residual Statistics
Which should we look at first?
Casewise diagnostics.
- This will identify the data that can be considered outliers according to the ‘standard error of prediction’.
- If there are any outliers that are more than 3 std devs beyond the value predicted by the regression line, then they can be considered ‘extreme outliers’ and should be removed
- Recalculate the regression with the outlier removed
How would you summarise what a scatterplot depicts?
A scatterplot depicts the nature of association between two variables in a graphical form
What is the difference between correlation and regression?
Correlation allows you to establish whether two variables covary, but does not enable prediction (regression does)
r = ?
degree to which X and Y vary together (covariability of X and Y) / Degree to which X and Y vary separately (Variability of X and Y separately)
What is the intercept?
a = the value of Yhat when X is zero
What correlation should you run if the data are non-parametric (e.g., curivlinear)?
Use Spearman’s correlation
What should you do before you run Pearson’s r?
Produce a scatterplot to see if data is linear and check for outliers. If appropriate then remove outliers.
What is this the formula for?
Standard error of estimate
It is the SD (sq root of variance - calculated by determing the variation between each data point relative to the mean) of predicted values and a common measure of accuracy of prediction
What is the mathematical formula for Pearson’s R?
rxy = cov(x,y)/SxSy
Standard deviation
- SD is a measure of spread
- A low SD tells us that the data is clustered around the mean, while a high SD tells us that it is dispersed over a wider range of values
- Used when the data is normally distributed
- Tells us whether a data point is standard/expected, or unusual/unexpected
- Represented by sigma
How to calculate:
- calculate the mean
- subtract the mean from each data point
- Square each difference
- Calculate the mean of the squared differences
- Take the Square root
How would you summarise what regression quantifies?
Regressions quantifies the degree of impact one variable has on another, thus enabling prediction
What is a positive correlation?
As one variable increases so the other increases
What is error variance in regression called?
Residual variance - it is the variability of predicted values
b = slope of line - change in predicted Y due to one unit change in X
What is this known as?
Regression coefficient
How do you run Pearson’s in SPSS?
Analyze –> Correlate –> Bivariate
This is the formula for the regression of the line.
How do you calculate a?
Describe Pearson’s Product-Moment Correlation Coefficient
The extent to which a criterion variable (Y) varies in conjunction with the predictor variable (X)
