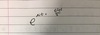Prob B Flashcards
(34 cards)
What is a random variable?
A quantity that is measured in an experiment with a random outcome, whose value depends of the experiment
Define a discrete distribution for a random variable

Define a continuous distribution for a random variable

Define the cumulative distribution function for both discrete and continuous functions

If Y = g(X), where X is a random variable and g: R to R, then what is the cumulative distribution of y with respect to Y, and the probability density function relationships

Define a joint distribution of X and Y
The join distribution of two random variables is defined on a sample space Omega with a probability measure P mapping B to P((X,Y) in B)
Define the probability of a joint distribution for discrete random variables

Define the probability of a joint distribution for continuous random variables

When are two random variables independent, state in terms of cumulative distributions

Define a convolution for mass and density functions

Define the exponential variable with parameter alpha

State and prove the memoryless property for an exponential variable
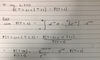
What is the gamma distribution with parameters n,alpha, and give the notation



Define the poisson counting process

Show by looking at P(Nt >= k) that Nt is a poisson random variable
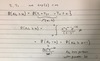
Define the expectation for a discrete distribution and a continuous distribution

Define the expectation of a discrete distribution for g(X) with f as mass function and g some given function. Prove

If the mass function is f for a continuous random random variable and g is a given function what is the expectation of g(X)
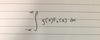
Define the bernoulli random variable

What is a moment generating function

If X and Y are random variables on the same sample space and g: R2 to R2 what is the expectation of g(X,Y) for both discrete and continuous cases

Prove that expectations are linear

State Fubini’s Theorem
If X and Y are independent then E(g(x)h(y)) = E(g(x))E(h(y))