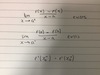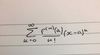Analysis Definitions Flashcards
What are the triangle inequalities for
i) |a+b|
ii) |a-b|
Give the definition of convergence for a sequence
When is a sequence cauchy
Give the definition of continuity
Give the definition of discontinuity
Give the definition of sequential continuity
Give the identity connecting x,sinx and tanx for an interval (0, pi/2)
0 < sinx < x < tanx
State the Intermediate Value Theorem
State the Extreme Value Theorem
If f: [a,b] to R is continuous then f is bounded above and below on [a,b]. There exists a x* and an y* in [a,b] such that f(x*) = inf(f(x)) and f(y*)=sup(f(x))
When is a subset A of R open
if for every x in A there exists an epsilon e such that (x-e,x+e) is a subset of A
When is a subset A of R closed?
if R \ A is open
Show the preimage of U, f-1U
When is a function f: A to B injective
f(x)=f(y) implies x=y
When is a function f:A to B surjective
For every y in B there exists an a in A such that f(a)=b
When is a function f:E to R increasing
x >= y implies f(x) >= f(y)
State the Inverse function theorem for continuous functions
Let I be an interval and suppose that f: I to R is continuous and strictly monotonic. Then J=f(I) is an interval and f-1: J to I is continuous and strictly monotonic
When is a function f:I to R injective if its continuous
If its strictly monotonic
Give the definition of a continuous limit
State and prove the sandwich rule for continuous limits
State and prove the continuous limits and composition proposition.
Give the definition of one-sided limits for a continuous limit
Define the conditions for f(x) tending to infinity as x tends to c
Give the two limits that must exist for a function f:(a,b) to R to be differentiable at x0 in (a,b)
State the Caratheodory formulation of differentiation
then f(x) = f(x0) = phi(x)(x-x0)
State and prove the chain rule
State the derivative of inverses theorem
State and prove L’Hopitals rule
When is a function right differentiable, left differentiable and differentiable
When is a function f continuously differentiable on an interval I
When f is differentiable on I and f’ is continuous on I
When is a function n times continuously differentiable
When f(n) exists and is continuous on I
When does a function f have
i) local maximum
ii) local minimum
State Rolles Theorem
State Taylor’s theorem
When f is continuously differentiable what is the taylor expansion of f about a
How do we show a taylor series expansion is convergent
Show that the remainder terms tend to zero
What are the series expansions for sinx and cosx
