Priority Queues and Heaps Flashcards
What is a priority queue and what are it’s operations?
What are the applications of a priority Queue?
Hospital emergency room
Event-Driven simulations
How does a priority queue compare to a queue?
What are the implementations of a priority queue, what are their speeds of operations and which is the best?
- Array or LinkedList
- order by priority (highest priority item first)
- DeleteMax is a remove-from-front(cost O(1))
- Insert is an ordered insert(cost O(n)
- order by priority (highest priority item first)
- Binary search tree (BST) The highest priority item is in the rightmost descendant of the root
- DeleteMax and Insert are O(n) (unless you use some sort of balanced tree (O(n)).
- Best-> a Heap: A binary tree - but not a BST - stored in an array
- DeleteMax and Insert are O(log n)
What is the definition of a full tree?
Define a complete tree
What is the definition of heap ordered?
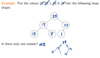
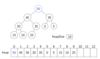
What is the definition of a heap
In general how is an array used to implement a heap?
With no pointers, how do we find a node’s children?
If 35 is stored in array index 5:
- What is the index of the left child?
- right child?
- What is the index of it’s parent?
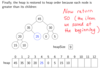
In general how do heap insertions work?
- First, place the new item in heap[heapSize] and increment heap size.
- The heap may not be heap ordered now (new item might be larger than parent)
- We need to sift up the new item towards the root
- repeatedly exchange the new item with it’s parent until either:
- It’s parent is larger than the new item, or
- The new item is the root
- repeatedly exchange the new item with it’s parent until either:
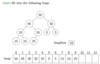
What is the code for insert (including the priority queue class)?
What is the code for siftUp?
What is the code for swap?
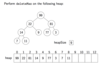
In general how doe DeleteMax work?
- Save the item in the roon (heap[0]), because it has the highest priority, so we will want to return it.
- Take the item I in heap[heapSize-1] (bottom of the heap) and place it in the root, and decrement heapSize.
- We must restore heap order in the heap: item I (which we just placed in the root) may be less than one or both of its children since an item fomr the bottom of the heap will have a low priority.
- To restore heap order: sift down the root (repeatedly swap I with the larger of it’s two children (if it has two) or it’s sole child (if only one) until either:
- I is larger than it’s two children(or than it’s sole and only child) or
- I has no children
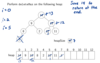
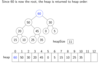
DeleteMax the following heap
What is the code for deleteMax?
What is the code for siftDown?
What is the run time of insert and deleteMax?
