Graphs

Question 1

What is the definition of a graph?

Answer 1

Question 2

What does adjacent mean in a graph? Draw an example.

Answer 2

Question 3

What is the definition of an undirected graph?

Answer 3

Question 4

What is the definition of a directed graph?

Answer 4

Question 5

Explain how a tree is a directed graph

Answer 5

Question 6

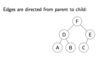
What is a path in a graph?

Answer 6

Question 7

What is a cycle in a graph?

Answer 7

Question 8

What does connected mean in a graph?

Answer 8

Question 9

What does it mean for a graph to be complete?

Answer 9

Question 10

What is a subgraph in a graph?

Answer 10

Question 11

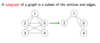
What type of information can the vertices represented in a graph?

What type of information can an edge represent in a graph?

Answer 11

Vertices

• The vertices in a graph may represent something(cities on a map, computers in a network)
• Vertices in a graph may contain information(information about the cities or computers represeted

Edges

• The edges may represent spatial connections between vertices or some other type of connection between the vertices.
• The edges may also contain information(distance between two cities, the cost of travel between two cities, capacity of a computer connection, weight of a connection in a neural network).
• If the information is a number, then the graph is called a weighted graph

Question 12

In general, what is an Adjacency Matrix?

Answer 12

Question 13

What is an example of an adjacency matric of an undirected graph?

Answer 13

Question 14

What is an example of an adjacency matrix of a Digraph

Answer 14

Question 15

What is an example of an adjacency matrix of a weighted graph?

Answer 15

Question 16

What are the advantages and disadvantages of an adjacency matrix?

Answer 16

Question 17

What is an adjacency list?

Show examples of undirected and digraphs.

Answer 17

Question 18

What are the advantages and disadvantages of an adjacency list?

Answer 18

Question 19

How do you decide to use an adjacency matrix or list?

Answer 19

Question 20

What is the definition and two types of a graph traversal?

Answer 20

Question 21

Perform a depth-first traversal of the following graph, draw the stack at each step.

What would the output be if we printed the contents of the vertex when we visit it?

Answer 21

Attached is an example of one step.

Output: 0, 1, 2, 4, 3, 6, 7, 5, 8, 9

Question 22

Display the output and the stack for a depth-first traversal of this graph starting at 6.

Answer 22

Question 23

Answer 23

Question 24

What is the Pseudocode for a depth-first traversal?

Answer 24

Question 25

What is a breadth-first traversal in a graph? Perform one on the following graph and print the output:

Answer 25

A breadth-first traversal visists all nearby vertices first before moving farther away. It is a queue-based, iterative traversal

Question 26

Answer 26

Question 27

Answer 27

Question 28

What is the Pseudocode for a breadth-first traversal?

Answer 28

Question 29

What needs to be done to record paths for a breadth-first traversal?

Answer 29

Question 30

Traverse the following example and show how you would record the path for a breadth-first traversal.

Answer 30

Question 31

What are connected components?

Answer 31

Question 32

How does a traversal work for unconnected graphs?

Answer 32

Question 33

What is the difference in the path that Depth-first and Breadth-first take?

Answer 33