Present Value Calculations - Week 2

Question 1

Valuing long-lived projects or securities :

Answer 1

Often the cashflow streams that we are interested in are comprised of multiple payments/receipts e.g.

• Stocks pay dividends on a regular basis
• Bonds make regular interest payments
• After making a loan to a friend you expect monthly repayments

We can use PV techniques to arrive at a total value for these cashflow streams. We can also use some shortcuts in certain cases to make our lives easier. Examples of these are;

• Annuities (with and with growth)
• Perpetuities (with and without growth)

Question 2

What is a perpetuity?

Answer 2

Consider an asset that promises a fixed nominal cashflow at the end of every period from now until the end of time.

i.e. interest rates are at 5% per annum and someone promises you $100 per year forever

Question 3

How to compute Present Values of perpetuities ?

Answer 3

Call the cashflow C and assume that the one-period interest rate is fixed at r.

Question 4

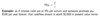
Perpetuity example: undated UK government debt :

Answer 4

War loans: in late 2014 and early 2015 the UK government repaid undated (perpetual) bonds that had been issued by previous UK governments to finance, amongst other things, the First World War.

Details: the WW1 debt was, in total around £1.9 billion with a 3.5% annual interest rate. The debt was perpetual and was originally issued in 1932.

Replacement: the undated debt was replaced with standard fixed lifetime gilts issued at relatively low interest rates (given current economic conditions). Plans were made and executed to take all undated UK bonds and replace them in the same way. Some of these other undated bonds were first issued in the 18th century.

Question 5

What are annuities?

Answer 5

These are more common cashflow streams, consisting of the payment of a fixed nominal cashflow, once per period but only for a known, finite number of periods.

Example: I promise to pay my mortgage company £10,000 per year at the end of each year for the next 25 years.

Question 6

How to compute the Present Value of an Annuity?

Answer 6

C= each year’s cashflow

Question 7

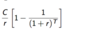
PV of annuities with payments at the beginning of the year?

Answer 7

Use the normal formula to find the PV_{<strong>A</strong>} and then:

Question 8

What is Perpetuities with growth ?

Answer 8

Another infinitely-lived stream of cashflows.

At the end of one period one is promised a cashflow of C and at the end of each subsequent period, the cashflow promised grows at rate g.

Thus the second cashflow is C(1 + g), the third is C(1 + g)² …..

Question 9

What is the formula of PV of Perpetuities with growth?

Answer 9

Notes:

• Clearly, we need r to be greater than g to make the answer to this infinite present value sensible.
• If g is above r then the cashflows grow more quickly than the discount factors and thus the sum is infinite.

Question 10

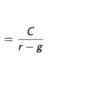
What are Annuities with growth?

Answer 10

Consider a cashflow stream such that at the end of one period one is promised a cashflow of C and at the end of each subsequent period, the cashflow promised grows at rate g. However, the cashflow stream terminates after T payments. This is an annuity with growth.

Valuation: use exactly the same trick as when valuing a no-growth annuity

• 1 Value a perpetuity with growth where the first payment is made one period from now.
• 2 Value a perpetuity with growth where the first payment is made T + 1 periods from now.
• 3 The cashflows from the annuity with growth equal the cashflows from (1) minus the cashflows from (2).
• 4 Thus the PV of the annuity with growth is the PV of (1) minus the PV of (2).

Question 11

What is the PV of Annuities with growth?

Answer 11

Valuation formula: if the first cashflow is C, the cashflows grow at rate g and the one-period discount rate is r then the PV of the growing annuity is;

Question 12

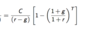
The effective (annual) interest rate is …

It’s formula is…

Answer 12

The actual interest you would receive on a deposit (or pay on a loan) on an annual basis, expressed as a percentage.

Used when, for example, the interest rate is compounded monthly, quarterly, semi-annually…

Question 13

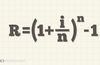
How to find the monthly, semi-annually… efffective interest rate when you’re given the annual effective interest rate?

Answer 13

r_M = (1 + r_A)^n/12 - 1

r_M= monthly interest rate

r_A= annual interest rate

n= number of cashflow period in a year

Question 14

Continuous compounding I

Formula for 1 year investment

Answer 14

Xe^r

r=interest rate

X=deposit amount

Question 15

Continuous compounding II

Formula for T years investment

Answer 15

Xe^rT

Question 16

Discounting in continuous time: you will receive a cashflow of X in T years. You want to compute the present value of the cashflow. If you are told that the continuously-compounded interest rate is r then the present value is;

Answer 16

PV = Xe ^-rT

Question 17

What are the inflation rate, nominal interest rate, and real interest rate?

Answer 17

Inflation rate: the (usually annual) rate at which the level of prices in the economy grows. Denote it by pi.

Nominal interest rate: the rate at which the balance of a deposit grows in cash terms. Denote it by r.

Real interest rate: the rate at which the balance of a deposit grows in purchasing power terms. Denote it by i.

Comments;

• Up to now we’ve worked entirely in nominal terms.
• If you’re given nominal cashflows, you should discount them at the nominal rate.
• If you’re given real cashflows, you should discount them at the real rate.

Question 18

Real interest rate formula =

Answer 18

Question 19

Approximate real interest rate formula =

Answer 19

i = r - pi

Question 20

Real and nominal interest rates III

Comments:

Answer 20