Introduction - Week 1 Flashcards
Some pearls of wisdom about theories and models:
- The purpose of theory is to predict and explain. A theory is not tested by the reasonableness of its assumptions but by its ability to predict accurately and explain.
Attribution Unknown
- A model is to be used, not to be believed.
Milton Friedman
How can I know if a theory is good or bad ?
- A theory is good if it matches the real world well
- A theory is bad if it matches the real world poorly
It is necessary to have a fair degree of skepticism regarding theories in general: they are not the truth and what works today might not work tomorrow..
Random variables and probabilities :
Risks and gambles are central to theoretical and practical finance. We will, therefore, rely on tools that describe gambles.
Random variables and possibilities outcomes Setup:
Consider a random variable Xi ;
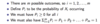
Summation: if you want to write the sum of Zi where i runs from 1 to K, we have;
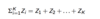
Product: similarly, if you want to write the product of Zi where i runs from 1 to K, we define;
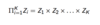
What is The expected value or mean of X ?
(Def. + Formula)
Its probability-weighted average
The mean measures the “average” outcome from a gamble or variable.
Why is the expected value or mean important for companies and investors?
- Investors are concerned with mean returns from portfolios.
- Companies care about expected values of cashflows from investment projects.
The variance of a random variable measures …
The (probability weighted) dispersion of the outcomes around the mean.
The more (less) spread out a variable’s outcomes are around its mean, the larger (smaller) the variance.
Formula of the variance:
Why is the variance important for investors?
Investors care about the variance of portfolio returns (as this is a measure of portfolio risk).
- The less spread out a variable’s outcomes are around its mean, the smaller the variance. Therefore, the ROI amount will be around the expected value of the mean. Investors know what they’ll get. Fewer risks.
- The more spread out a variable’s outcomes are around its mean, the larger the variance. Therefore, the investors can expect higher returns (far above the mean) but also smaller return or losses (far under the mean). More risks.
What is the Discount Rate?
Interest rate used to compute present values of future cash flows
What is the Discount Factor?
Present value of a $1 future payment
What is the Present Value?
Value today of a future cash flow
What is the Future Value?
Amount to which an investment will grow after earning interest.
A discount rate is…
The reward that investors demand for accepting delayed rather than immediate gratification.
The discount rate is also called:
- Interest rate
- Required rate of return
- Opportunity cost of capital.
What is the discount rate in real life?
- If you lend someone money for a year, you demand interest as you cannot instantly spend the money you have lent on consumption goods.
- If you lend money to a less trustworthy person/company, you require a greater interest rate as you’re less confident that you’ll get your money back.
- The discount rate is also called opportunity cost of capital because it is the return foregone by investing in a capital project rather than investing in freely-available securities.
How many varieties of interest calculation are there?
2
Simple and compound interest.
What is the simple interest?
The interest earned or paid is just the original balance of the deposit/loan (X) times the interest rate (r).
So over T periods, the total balance of your deposit/debt will grow to be: X + r × X × T =
X (1 + rT ).
What is the Compound Interest?
Interest must be paid on previously charged/earned interest.
So over T periods, the total balance of your deposit/debt will grow to be:
X(1+r)T
r=interest rate
T=time
Compound versus simple interest at 10% per annum :
Clearly: compound interest is good for savers (bigger sum earned) but worrying for borrowers (higher monthly/annual payments)
What type of question asks for the future value of X, assuming an interest rate of r and an investment period of T ?
We are given a cashflow of X today. What value will this cashflow grow to if invested at interest rate r for T periods?
FV (r,T) = X (1 + r )T
- Obviously, the future value is larger if r is larger
- The future value is obviously also greater when T is greater or when X is greater.
Future value: example
How can we explain the Present Value ?
- Assume that you’re due to receive a payment of X in T years.
- What current cashflow is equivalent to that future cashflow?
- Compute the amount that you would have to place in a bank today such that it would grow to be exactly worth X in T years.
- Equivalently, how much would a bank lend you today if you promise to give them a repayment of X in T years.
How to compute the Present Value?
Or X x (1 + r)-T
When computing present values we often make use of an object called a …
Discount Factor
- A discount factor is just the present value of £1.
- Discount factors vary with the interest rate and with the investment horizon.
- Higher interest rates lead to lower discount factors and longer investment periods lead to lower discount factors
We calculate a discount factor as :
Present values and discount factors: using the definition of the discount factor we can rewrite the present value as:
PV(r,T) = DF(r,T) × X
Positive cashflows are :
Receipts
Negative cashflows are :
Payments
Until now we’ve thought about single cashflows (current or future) only.
Most investments or applications involve multiple cashflows received and paid at different points in time.
How do you compute present values for these more complicated streams of money?
This is called the Net Present Value or NPV.
Take each individual cashflow and compute its present value.
Sum present values across all of the cashflows.
(Receipts will contribute positively to NPV and payments will contribute negatively.)
How to Calculate the NPV ?
(Assume a constant interest rate of r per period. Assume a investment project which will deliver a cashflow of C1 at the end of 1 period, C2 at the end of two periods, continuing until it finishes by delivering a cashflow of CK after K periods)
The NPV rule:
Consider a financial or physical investment project for which you have calculated the NPV
- If the NPV is positive you should invest in the project.
- If the NPV is negative, you should turn down the investment opportunity.
Comments on the NPV:
- The discount rate used in the NPV calculation should reflect the project’s risk: more risky projects require a greater return and so you should use a larger discount rate.
- If you don’t know the cashflows associated with the project precisely, use the expected value of each cashflow instead.
Why is it optimal for individuals to invest in projects with positive NPV and discard projects with negative NPV?
It turns out that NPV is optimal (under some assumptions) in the sense that use of the rule leads to investors maximising their expected wealth.
This is true regardless of how patient or impatient an investor is, and thus the rule can be used for all investors (they will all agree on which investments to choose and which to discard).
