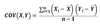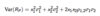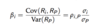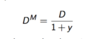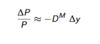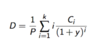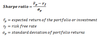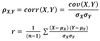Formulas Revision

Question 1

Variance

(With proba + with historical data)

Answer 1

Question 2

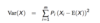
Simple Interest=

Answer 2

X(1 + rT)

Question 3

Future Value

Answer 3

X(1 + r)^T

Question 4

Present Value (2)

Answer 4

DF * X

Question 5

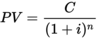
Discount Factor

Answer 5

PV of $1

Question 6

Net Present Value

Answer 6

Question 7

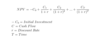
PV Perpetuity

Answer 7

Question 8

PVp₂ = value of a perpetuity paying C per year with first payment in T+1 years

Answer 8

Question 9

PV of an annuity: (3)

Answer 9

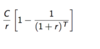
• PV_p - PV_p2
  *

Question 10

PV of an annuity paid at the beginingof the year

Answer 10

PV_a * (1 + r)

Question 11

PV_p with growth

Answer 11

Question 12

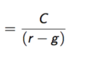
PV_a with growth

Answer 12

Question 13

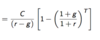
Effective Annual Rate

Answer 13

Question 14

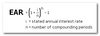
Effective Monthly Rate

Answer 14

Question 15

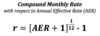
Continuous Compounding

Answer 15

Xe^r

Question 16

Continuous discounting

Answer 16

PV= Xe^-rT

Question 17

Real interest rate

Answer 17

(1+r)/(1+pi)

i=real interest rate

r=nominal interest rate

𝜋(pi)=inflation rate

Question 18

Approximate Yield To Maturity

Answer 18

Question 19

Relationship formula YTM/PV

Answer 19

Question 20

Gordon Growth Formula

Answer 20

Question 21

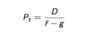
Stock Price with constant dividend

Answer 21

Question 22

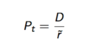
Return on Equity/Return on investment

Answer 22

= Amount of earnings a dollar of equity creates

EPS= earning per share

Question 23

Earning growth

Answer 23

Plowback ratio = 1 -payout ratio

Question 24

Nominal Interest rate =

Answer 24

Real rate + Inflation

Question 25

Forward Rate

Answer 25

Question 26

Standard Deviation

Answer 26

Racine carrée of Variance

Question 27

Inflation rate is written as:

Answer 27

pi

𝜋

Question 28

Above and Below Par:

Answer 28

Above par = coupon rate > YTM

Below par = coupon rate < YTM

Question 29

A zero-coupon bond…

Answer 29

Receive money only at maturity

Question 30

PV of growth opportunities:

Answer 30

P₂ - P₁

Form reinvesting VS firm paying out

Question 31

Covariance formula

Answer 31

Question 32

Expected Portfolio Return

Answer 32

x_i = portfolio weight allocated to asset i

y_i = mean/expected return on asset i

Question 33

Variance of portfolio

Answer 33

ex. with 2 assets

Question 34

Beta asset

Answer 34

• If you slightly increase the portfolio weight on stock i then the overall portfolio variance would increase by an amount proportional to Bi
• If Beta is 0.4, for every 1% rise (fall) in the market, you expect the stock to rise (fall) by 0.4%
• B > 1 = Aggressive; moves with the market but with greater amplitude

Question 35

Beta portfolio

Answer 35

Question 36

US risk premium

Answer 36

Difference between mean annual stock market return and T-Bill return

Question 37

Portfolio weights and risk free asset

Answer 37

Question 38

Annual (arithmetic) return

Answer 38

(P₁ - P₀ + D₁) / P₀

P₁ = new price

P₀ = ancient price

D₁ = dividend

Question 39

Capital Gain =

Answer 39

(VA - VD) / VD) * 100

Question 40

Dividend Yield

Answer 40

Question 41

Excess Return

Answer 41

R - Rf

(annual return - risk-free)

Question 42

Present Value of Growth Opportunities

Answer 42

Difference in value between the firm that plows back and the one who does not

Question 43

Modified Duration (or Volatility)

Answer 43

Question 44

Yield changes by (delta)y

Answer 44

Question 45

Duration/Macaulay Duration

Answer 45

Question 46

Risk free asset property

Answer 46

• Rf Variance and Covariance = 0

Question 47

CAPM (Capital Asset Pricing Model)

Answer 47

Question 48

Sharpe Ratio

Answer 48

Question 49

Correlation

Answer 49