Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

CFA Level 2 > Portfolio Management > Flashcards

Portfolio Management Flashcards

1
Q

Arbitrage Pricing Theory (APT) - value of Ri

A
  • the intercept is the expected return of asset i given that all the other factors take on a value of 0
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

APT assumptions

A
  • A factor model describes asset returns
  • There are many assets, so investors can form well-diversified portfolios that eliminate asset-specific risk, not factor risk
  • No arbitrage opportunities exist among well-diversified portfolios
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

APT E(Rp) given that the 3 assumptions of the model hold

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

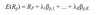
Pure factor portfolio (or factor portfolio)

A

A portfolio with a sensitivity of 1 to factor j and a sensitivity of 0 to all other factors

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Carhart four-factor model notation (extension of the Fama and French model)

A
  • RMRF = the return on a value-weighted equity index in excess of the one-month T-bill rate
  • SMB = small minus big, a size (market capitalization) factor; SMB is the average return on three small-cap portfolios minus the average return on three large-cap portfolios
  • HML = high minus low, the average return on two high book-to-market portfolios minus the average return on two low book-to-market portfolios
  • WML = winners minus losers, a momentum factor; WML is the return on a portfolio of the past year’s winners minus the return on a portfolio of the past year’s losers
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Carhart four-factor model / Rp - Rf

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Carhart four-factor model / E(Rp)

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

Types of multifactor models

A
  • Macroeconomic
  • Fundamental
  • Statistical:
    • Factor analysis - best explain historical return covariances;
    • Components models - best explain historical variances
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

bik for the fundamental factor model

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Active return formula

  • Asset allocation or sensitivity factor
  • Security selection factor
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Information ratio (IR)

A
  • = Active return / Active risk
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

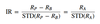
Active risk (also called Tracking error (TE)) - formula

A
  • s(Rp - RB)
  • s(RA)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Active risk squared (active risk is also called tracking error or tracking risk) - formula

A

s2 (Rp - RB)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Active risk squared decomposition

A
  • Active risk squared = Active factor risk + Active specific risk
  • Active factor risk and active specific risk refer to variances rather than standard deviation
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q
  • Active factor risk
  • Active specific risk or security selection risk
A
  • The contribution to active risk squared resulting from the portfolio’s different-from-benchmark exposures relative to factors specified in the risk model
  • The contribution to active risk squared resulting from the portfolio’s active weights on individual assets as those weights interact with assets’ residual risk
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Portfolio alpha

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

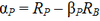
Active specific risk formula

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

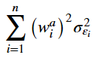
Active specific risk notation

A
  • wai is the ith asset’s active weight in the portfolio (that is, the difference between the asset’s weight in the portfolio and its weight in the benchmark)
  • σ2εi is the residual risk of the ith asset (the variance of the ith asset’s returns left unexplained by the factors)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Value added formula

A
  • RAi = Ri - RB
  • Ri = return to asset i
  • RB = return on the benchmark portfolio
  • Δwi = wP,i – wB,i
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

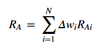
Value added as the sum of the active asset allocation decisions and the weighted sum of the value added from security selection, RA,j = RP,j – RB,j, within each asset class

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q
A

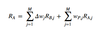
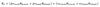
The first (parenthetical) term above is the value added from the asset allocation decision. The second term is the value added from security selection within the stock and bond portfolios. The active weights in the first term refer to differences from the policy portfolio

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Sharpe ratio

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

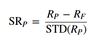
Sharpe ratio for leveraged portfolio

  • STD of the risk-free cash (1 - wp) is 0
  • RC = wPRP + (1 – wP)RF
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

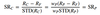
(Sharpe ratio)2p

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

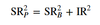
The level of active risk that leads to the optimal result for unconstrained portfolios

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

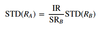
The level of active risk that leads to the optimal result for constrained portfolios

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

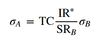
Maximum value of the constrained portfolio’s squared Sharpe ratio

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q

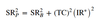
The total risk of the actively managed portfolio is the sum of the benchmark return variance and active return variance

29
Q

Mean–variance-optimal active security weights for uncorrelated active returns

30
Q

Grinold rule

A
  • Si represents a set of standardized forecasts of expected returns across securities (also called scores)
  • σi are multipliers (separate values for individual securities)
  • μi are the forecasted active returns
31
Q

Mean–variance optimal active weights using the Grinold rule

32
Q

Information coefficient (IC) - formula

/

IC is the ex ante risk-weighted correlation

33
Q

E(RA)* - optimal expected active return

34
Q

IR* - information ratio of the unconstrained optimal portfolio

35
Q

E(RA) of the full fundamental law

36
Q

Transfer coefficient (TC) - definition

A

The TC is the cross-sectional correlation between the forecasted active security returns and the actual active weights, adjusted for risk

37
Q

Transfer coefficient (TC) - formula

38
Q

Information ratio (IR) of the full fundamental law

39
Q

The expected value added conditional on the realized information coefficient, ICR

40
Q

Realized active return RA considering noise - formula

41
Q

The IR for a constrained portfolio generally decreases

A

With the aggressiveness of the strategy

42
Q

Active return does not equal alpha

A

RA = RP – RB, while αP = RP – βP × RB

43
Q

Unconstrained Portfolio

A

An investment style that does not require a fund or portfolio manager to adhere to a specific benchmark. Unconstrained investing allows managers to pursue returns across many asset classes and sectors

44
Q

μi - the security’s expected active return

A

μi = E(RAi)

45
Q

Active weights

47
Q

RAi as the residual return in a single-factor statistical model

48
Q

Aggressiveness of the active weights impact on the information ratio

A
  • The information ratio is unaffected by the aggressiveness of the active weights (deviations from benchmark weights) because both the active return and the active risk increase proportionally
  • The aggressiveness will only decrease the IR of a constrained portfolio
49
Q

Portfolio variance

50
Q

Portfolio variance for a portfolio with equal weights 1/N

A
  • σ2 overlined = average variance
  • Cov overlined = average covariance
51
Q

Capital allocation line (CAL)

52
Q

Capital market line (CML)

53
Q

Capital market line (CML) versus capital allocation line (CAL)

A

The capital market line (CML) is the capital allocation line formed when the risky asset is a market return rather than a single-asset return

54
Q

Portfolio variance for a portfolio of two assets

55
Q

CAL and the Sharpe ratio

A

The Sharpe ratio is the slope of the CAL

56
Q

Markowitz efficient frontier

A
  • The graph of the set of portfolios offering the maximum expected return for their level of risk (standard deviation of return)
    *
57
Q

Market model (single-index model) - return, variance and covariance

58
Q
  • Factor portfolio
  • Tracking portfolio
A
  • A portfolio with a factor beta equal to one for one factor and zero for all other factors. Factor portfolios have higher active factor risk (which refers to the deviation of a portfolio’s factor betas from those of the benchmark)
  • A portfolio with factor betas equal to those of the benchmark
59
Q

Macroeconomic models

A
  • The intercept ai is the expected return to stock i
  • All other factors have an expected value of 0 and represent a surprise
60
Q

Ex post IR

A
  • = tb0 / (number of observations)1/2
  • = t-value for the intercept / square root of the number of observations
61
Q

Value added from α

A
  • α = IR * ω
  • VA = α - (λ - ω2)
  • ω = residual risk
  • λ = risk aversion
  • α = expected value of the active return

*tested in 2015

62
Q

Information ratio from α

A
  • IR = α / ω
  • ω = residual risk
  • α = expected value of the active return
63
Q

Information ratio additivity

A
  • IRnew2 = IRa2 + IRb2
  • The IR of the new stocks can simply be added to the IR of those already managed
64
Q

Portfolio constraint

A
  • Time horizon
  • Liquidity
  • Tax concerns
  • Legal and regulatory factors
  • Unique circumstances
65
Q

The alpha and information ratio of a portfolio consisting of only cash and the benchmark

A

Both the alpha and the information ratio are 0

66
Q

IC using the number of successful decision

A
  • IC = 2(Nc / N) - 1
  • Nc = number of correct decisions
  • N = total number of decisions
67
Q

Sharpe ratio and cash

A

The Sharpe ratio is unaffected by the addition of cash or leverage in a portfolio and would thus not be appropriate to evaluate a portfolio in which an allocation to cash was a key part of the investment decision process

68
Q

The Fundamental Law of Active Management separates the expected value added, or portfolio return relative to the benchmark return, into the basic elements of the strategy

A
  • Skill (information coefficient)
  • Portfolio construction (transfer coefficient)
  • Breadth (number of independent decisions per year)
  • Aggressiveness (benchmark tracking risk)

CFA Level 2 (13 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions