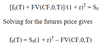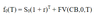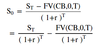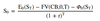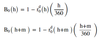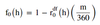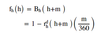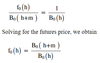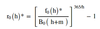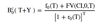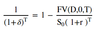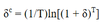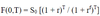Futures and Forwards

Question 1

NDFs

Answer 1

Nondeliverable forwards

Question 2

Total return index

Answer 2

Dividends are reinvested into the underlying index

Question 3

Eurodollar

Answer 3

• US dollar deposits held outside the USA. Based on the LIBOR
• The long position locks in a fixed rate

Question 4

FRA payoff

Answer 4

Question 5

FRA quotation

Answer 5

A * B

• Contract expires in A months
• At expiration the tenor is (B - A)
• Total duration is B

Question 6

• FRA price
• FRA valuation

Answer 6

• Amount to pay in order to enter the FRA
• Amount to pay or receive in order to exit once held

Question 7

Forward value at initiation - formula

Answer 7

Question 8

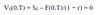
Forward value at time t - formula

Answer 8

Question 9

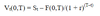
Off-market FRA

Answer 9

The initial value isn’t necessarily set at 0

Question 10

F(0, T) for an underlying paying dividends

Answer 10

PV(D, 0, T) = present value of dividends (actualized from the ex-dividend dates or the actual dividend payment date)

Question 11

Continuously compounded risk-free rate

Answer 11

Question 12

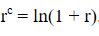
Discrete to continuous

Answer 12

Question 13

Price of a forward paying a constant dividend at rate delta^c

Answer 13

S₀ is discounted at the dividend yield rate and equals the present value of the stock without the dividends

Question 14

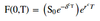
F(0, T) on a coupon-paying bond

Answer 14

• PV(CI, 0, T) = present value of the coupons
• T = time to expiration
• Y = remaining time to maturity at expiration

Question 15

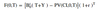
V_t (0, T) for a coupon-paying bond

Answer 15

• The contract expires in T days
• After expiration, the bond has a tenor of Y days

Question 16

FRA notation

Answer 16

• g - an arbitrary day prior to expiration
• h - the expiration day
• h + m - time until the maturity of the Eurodollar instrument on which the FRA is based
• L_i (j) - the rate on a j-day LIBOR deposit on day i

Question 17

FRA payoff using notation

Answer 17

Question 18

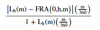
FRA (0, h, m) in function of the Libor rate - formula

Answer 18

Question 19

FRA - V_g (0, h, m) formula

Answer 19

Question 20

F (0, T) - Interest rate parity

Answer 20

Question 21

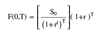
F (0, T) for a continuously compounded currency forward

Answer 21

Question 22

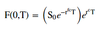
V_t (0, T) for a currency forward

Answer 22

Question 23

V_t (0, T) for a continuously compounded currency forward at time t

Answer 23

Question 24

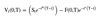
Variation margin

Answer 24

The margin that must be deposited to get back to the inital margin requirement

Question 25

Price limits

Answer 25

* Limit move - when the price is frozen at one of the limits * Limit up, down * Limit locked - when the transaction can't take place

Question 26

EFP

Answer 26

Exchange For Physical

Question 27

Scalper

Answer 27

A trader that attempts to profit from buying at the bid price and selling at the higher ask price

Question 28

Conversion Factor

Answer 28

A factor used to equate the price of T-bond and T-note futures contracts with the various cash T-bonds and T-notes eligible for delivery. This factor is based on the relationship of the cash-instrument coupon to the required 6 percent deliverable grade of a futures contract as well as taking into account the cash instrument's maturity or call

Question 29

Cheapest-to-deliver

Answer 29

In a futures contract, the cheapest security that can be delivered to the long position to satisfy the contract specifications. The cheapest to deliver security is relevant only for contracts which provide that a variety of slightly different securities may be delivered

Question 30

Futures values

Answer 30

Question 31

In general, the futures price is the spot price compounded over the life of the contract, T years, at the annual risk-free rate, r

Answer 31

f₀(T) = S₀(1 + r)^T

Question 32

f₀ (T) including cash flows

Answer 32

Question 33

f₀ (T) including storage costs

Answer 33

Question 34

Futures price including the cost of carry

Answer 34

CB = costs of storage - non-monetary benefits (convenience yield)

Question 35

* Contango * Backwardation * Normal Contango * Normal Backwardation

Answer 35

* Futures price are above the spot price * Futures price are below the spot price * Futures price above the expected spot price * Futures price are below the expected spot price

Question 36

S₀ in function of the present value of S_T and FV(CB, 0 , T)

Answer 36

Question 37

S₀ in function of E [S_T] plus a risk premium

Answer 37

Question 38

FV(CB,0,T)

Answer 38

Costs of storage – Nonmonetary benefits (Convenience yield)

Question 39

* r₀^d (h) * r₀^d (h + m)

Answer 39

Question 40

B₀ (h) and B₀ (h + m) in function of the discount rate

Answer 40

Question 41

f₀ (h) in function of r₀^df (h)

Answer 41

Question 42

T-bill futures at expiration

Answer 42

Question 43

Relationship between f₀ (h) and B₀ (h + m)

Answer 43

Question 44

* r​^df₀ (h) * f₀ (h) * B₀ (h)

Answer 44

* implied discount rate on day 0 of a futures contract expiring on day h, where the deliverable instrument is an m-day T-bill * price on day 0 of a futures contract expiring on day h * price on day 0 of the T-bill maturing on day h

Question 45

The implied repo rate

Answer 45

Question 46

Implied discount rate by the futures price as a ratio of (h + m) and (h) T-bill maturities

Answer 46

Question 47

B₀^c (T + Y) price

Answer 47

Question 48

B₀^c (T + Y) when considering the conversion factor

Answer 48

Question 49

f₀ (T) for a coupon paying bond

Answer 49

Question 50

f₀ (T) for a coupon paying bond when considering the conversion factor

Answer 50

Question 51

f₀ (T) for a stock index paying dividends

Answer 51

Question 52

Definition of delta as the dividend yield

Answer 52

Question 53

f₀ (T) using delta

Answer 53

Question 54

f₀ (T) using delta\*

Answer 54

Question 55

Delta^c - continuous to add-on

Answer 55

Question 56

Formula to use to find the arbitrage-free exchange rate

Answer 56

Question 57

The rates implied by Eurodollar futures will differ from the forward rates implied by T-bills because

Answer 57

Eurodollar securities have add-on interest and T-bills are discounted

Question 58

Roll return relation to backwardation and contango

Answer 58

* Positive if the market is in backwardation * Negative if the market is in contango