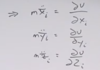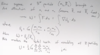Newton’s law of gravitation, N-body problem, Two-body problem Flashcards
What is Newton’s First Law?
If the resulting force F_vector on a particle is zero, then the particle will have constant velocity.

What is Newton’s Second Law?
If F_vector is not equal to zero, then F_vector is proportional to the time derivative of the particle’s momentum.

What is Newton’s Third Law?
For each action (force) exerted upon one particle by another, there is an equal and opposite reaction force on the other body.
Newton’s Law of Universal Gravitation
Any two bodies attract one another with a force proportional to the product of their masses and inversely proportional to the square of the distance between them.
{R1}_vector: inertial positon of m1
{R2}_vector: inertial postion of m2

What is G?
Gravitational constant
G = 6.67 x 10-11 [m3/kg*s3]
empirically derived
What is the force acting on M1? And then on M2?

What is the sum of the forces for the two-body problem?
zero

What is the N-body problem?
In an N-body system, any acceleration of one point mass is due to all the graviational forces from the other masses that are in the system.
The sum of all of the forces is still zero (conservative).
In a system of particles, each particle may feel both external and internal forces. Here, external forces are forces from external sources, while internal forces are forces between particles in the system. Since the sum of all internal forces will be 0 due to the Newton’s 3rd law

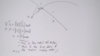
What is the center of mass?

What can you say about the center of mass of the system?
CoM motion is linear (see image for proof).
By introducing the concept of COM, the translational motion becomes that of a point particle with mass m. This simplifies the mathematical complexity of the problem.
C1t + C2 (CoM can also be still C2)

How many kinematic quantities must we evaluate over time to completely determine the evolution of the state of the system of N bodies?
6*N
(3 positions + 3 velocities)
Can we easily solve for the state of the N-body system? Why?
Need same number of equations as the number of unknowns (6*N).
10 Integrals of Motion (C1 vector (3), C2 vector (3), C3 vector (3), and C4 scalar)So for a 2-body system, we would need 6*2 = 12 first order diff. equations so the 10 integrals of motion would not be enough.
We have an analytical solution to the 2-body problem. We have solutions to several restricted 3-body problems, but no general analytic solution.

Restrict questions to 2-body problem. Using Newton’s 2nd law of motion and the universal law of gravitation, derive the dynamic equation of the motion of body M2 relative to body M1. How many integrals of motion do we need to fully characterize the motion of M2 relative to M1? Why?
Result is a system of differential equations of order 6 ( components of r vector are defined by a system of 3 coupled equations of order 2)
Proof that linear momentum is constant

If linear momentum is constant then there is…
conservation of momentum.
Proof that sum of moments of momentum, or angular momentum is constant.
(hint: cross-product of R)

Solution to taking the dot product of {Ri}_vector_dot of newton’s law of universal gravitation (eqn A) and summing over all sets


For a 3 Body system (i=3 & j=3), write out n-body equation simplified.

Why is there a 1/2 in the summation notation for the N-body system expression?

Derive eccentricity (scalar)

Kinetic Energy Equation

Potential Energy Equation
Note: Prof Gunther’s notes is U = -(V) = +
Prof Ho’s notes is V
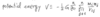
Equation for the conservation of energy of the system
T + V = C4
(Prof Ho’s notation)
or
T - U = eccentricty
(Prof Gunter’s notation)
- conservative system
10 constants of motion