NEW EXAM - POWER Flashcards
Define statistical power / What is the power of a test?
Power is the probability of rejecting the null hypothesis when it is false; or, in other words, the probability of declaring an effect to be significant when it is genuinely present
The power of a test is the probability of detecting H1 assuming it is true (ie detecting a real effect).
Conventional level for good power?
A conventionally acceptable level of power is 80%.
(or 0.8 / 0.9)
no other answers get any marks esp. if they talk about effect sizes
What is a simple and widely-used measure of effect size?
cohen’s D as an appropriate effect size indicator
What effect sizes are regarded as small medium or large (conventionally)?
Cohen’s conventional benchmarks (0.2- is small 0.5 medium 0.8+ is big)
How to calculate effect size?
Mean of Exp group - Mean of Control Group
/
common standard deviation
Cohen’s d is the mean difference between two means being compared divided by the common standard deviation (assuming means drawn from populations with homogeneous variances)
Factors affecting power?
- running the test 1-tailed (it says that the simulations given are 2-tailed) 1-tailed INCREASES power cf 2-tailed
- (larger effect size INCREASES power)
- changing the alpha level (counting only results below p=0.01 as significant). Lower p value gives LOWER power.
- Smaller standard deviations INCREASES power (This must be done keeping the mean separation same, this is effectively another way of decreasing/increasing effect size) - precision and variation (inverse variance) = more precise a data spread is, the greater the power!
- Sample size - increase the sample size as this not only reduces the standard error (less variance) but increases the effect size (if there is one)
What is the relationship between power and type-2 errors?
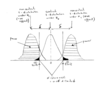
(May illustrate the rest of this answer with an appropriately and fully labelled diagram to replace much of the text below.)
Type II errors are the probability of accepting the null hypothesis when it is false. If type II errors occur at a rate of beta %, then power is (1 – beta)%.
Describe power’s relationship with non-central distributions
Power relates to the case when the null hypothesis (H0) is false. This situation reflects a different set of distributions (non-central distributions) whereas standard statistics are estimated against the situation when H0 is assumed to be true, and the associated distributions (central distributions).
Imagine a situation in which of a mean difference between two groups, D, where D0 is the value expected under H0 and D1 is the value expected under the alternative hypothesis (H1).
H0 implies that D0=0 whereas H1 implies that D1 is not equal to 0. The quantity (D1-D0) is known as delta, the non-centrality parameter.
In planning and executing your experiment what can you do to increase power? (6)
1 mark each for:
- Using a more lax alpha value (0.05 rather than 0.01)
- Increasing sample size
But one extra mark for each of the following (up to a maximum of 3 marks):
- Using a one-tailed test rather than a two-tailed test where appropriate
- Using equal sample sizes between groups where possible
- By doing all you can to increase the reliability of your variables (reducing sources of error variance)
- Using experimental manipulations which are likely to produce the largest effect size possible
What information do you need in order to estimate sample sizes before embarking upon a study?
- (1.5 marks) A desired level of power (usually 80 or 90%)
- (1.5 marks) The alpha level to be used (0.05)
- (1.5 marks) An estimate of the MINIMAL (must state minimal or smallest for full 1.5 here) effect size that you would want to be able to detect or that is likely to occur in your experimental setup
- (0.5 marks) A knowledge of whether the hypothesis to be tested is directional (1-tailed) or not
How might you obtain the information required for the sample size estimation process in (iv)?
You can get the info required to estimate sample size by convention (alpha and desired power) (2 marks)
Plus 3 ways to estimate the effect size
(3 marks in total; 1 for each way)
- by a pilot study or use of published previous results
- by convention (Cohen’s d: small effect size 0.2; medium 0.5; large 0.8+)
- by expert opinion, although the expert will be unlikely to phrase their opinion in terms of effect size so you will have to convert their views into an effect size. Eg a clinician might say that the minimum effect that we would want such a treatment to produce (given its cost) is a 15% decrease in depression ratings on the standard questionnaire
What is the non-centrality parameter?
In the question they asked “the non-centrality parameter shown is equal to (0.5*d2*n)” to check calculations - so how would one calculate effect size, and then work this out?
noncentral distributions describe the distribution of a test statistic when the null is false (alternative hypothesis). This leads to their use in statistics, especially calculating statistical power.
So calculate cohen’s d by taking difference between non-smk and smokers and divide by the average of the two standard deviations
Then do 0.5 x cohen’s d squared x number of participants
for 2 marks: Cohen’s d is the mean difference between two means being compared divided by the common standard deviation (assuming means drawn from populations with homogeneous variances)
for 2 marks per DV: I will do the calculation for lung capacity; answer should give both; give some credit for correct approach even if calculation error appears in working.
Mean difference in lung capacity = 17.74 – 15.98 = 1.76
s. d. of lung capacity in nonsmokers = 2.57
s. d. of lung capacity in smokers = 2.71
these s.d. look quite similar so are likely to be homogenous; we could base the calculation on either value or the average of the two (better) = 2.64
d = 1.76 / 2.64 = 0.67
Check for 1 mark per DV: must be shown for each for full marks
ncp = 0.5*d2*n
n=40
my estimate of d is 0.67
thus my estimate of the ncp is 0.5*0.67*0.67*40 = 8.978, which checks (within calculation error) with the printed value of 8.833
Explain in words what information is conveyed by the observed power results. How might this information bear on the researcher’s conclusions about the hypotheses under test?
From Internet
Observed power (or post-hoc power) is the statistical power of the test you have performed, based on the effect size estimate from your data. Statistical power is the probability of finding a statistical difference from 0 in your test (aka a ‘significant effect’), if there is a true difference to be found. Observed power differs from the true power of your test, because the true power depends on the true effect size you are examining. However, the true effect size is typically unknown, and therefore it is tempting to treat post-hoc power as if it is similar to the true power of your study.
From Alan Exam
- The observed power results tell us that, if the true effect size is exactly equal to the observed effect size (this is the key part here), then this is the power one would have to detect those effects for a 5% two-tailed test in samples of this size.
So, for lung capacity we would have an 83.5% chance of detecting the observed effect size in samples of 40 smokers vs. 40 nonsmokers.
The observed power for smellid (23.1%) appears to be very low. However, this reflects the fact that a small observed effect size (below 0.3) was obtained. This result might suggest that the true effect size is small, but of course through sampling error this study might have considerably underestimated the true effect size. This illustrates the limited value of observed power, as we might actually be concerned only with power to detect larger effect sizes. So actually, this observed power information is likely to have very little bearing on the researcher’s conclusions.
Explain, using a suitably annotated table or graph, the relationship between Type II error rate and power. Also explain the influence of Type I error rate on power. (10 marks)
Draw a fully-labelled diagram which depicts the distributions of the mean difference in volume under the null hypothesis and under an alternative hypothesis in which the mean difference in volume is different from zero. The diagram should indicate the areas under the distributions which correspond to power, and the proportions of type I and type II errors. (20% marks)
A really good answer should explain what the means (μ0 and μ1) are and what the hypotheses (H0 and H1) are. The means are the values of the mean difference between the groups on the measure of interest under the relevant hypotheses (H0 states that the mean difference is zero; H1 that it is different from zero
What conventional values of power could the researcher use?
- Give 0 marks for anyone who mistakenly quotes Cohen’s rules of thumbs for effect sizes (0.2 small; 0.5 medium; 0.8+ large)
- 80% or 90% are usual for sample size determinations.
The final line of the syntax uses the NCDF.T function from SPSS. This is the cumulative distribution function for a non-central t-distribution. Explain, with the aid of a suitably labelled diagram, how the non-central t-distribution is related to the standard t-distribution, indicating which feature of the diagram corresponds to delta.
The middle line of the syntax computes a critical t-value (as a variable called tcrit). Mark on the diagram approximately where tcrit would appear for a standard value of alpha (=0.05). Shade and label areas under the distributions corresponding to alpha and power.
