NEW EXAM ANCOVA Flashcards
What are the three specific assumptions for ANCOVA?
- The covariate needs to be independent of treatment (not correlated with any IV in a meaningful way)
- Homogeneity of regression slopes (HOR) for each group – relationship between the DV and the covariate has to be same for each group. This is because the ANCOVA takes the overall slope (e.g. slopes in the pics provided are all parallel) and applies to all IVs.
- The covariate is measured with as little error as possible (reliable covariates e.g. if you measured IQ really badly – like with one question 2x2)
To control for experimentwise Type I error rate at 0.05, each of the three univariate analyses was conducted at a per comparison rate of 0.017.
Which post hoc procedure was employed here? Mention an alternative test.
a priori contrasts specified in spss prior to the analysis
What is the sample size calculation for studies with low N and covariates?
{C+(J-1)}/N
(Groups - 1) + number of covarites - divided by the total sample size
C = number of CV
J = number of Groups
N = total sample size
So, for a 3-group problem with a total of 60 subjects, C < 4
If too many CVs are used, the estimates of adjusted means will be unstable
– For small group sizes, power will be poor so one should attempt to reduce the error variance and to increase the sensitivity
Legitimate ANCOVA requires
RANDOM ASSIGNMENT OF GROUPS
Briefly, how does ANCOVA increase power?
What happens to the F ratio?
ANCOVA removes the portion of the DV variation, explained by the covariate, from the error term and thus increases statistical power to assess the effects of the group factor(s).
F ratio is going to be larger, because the error term will be smaller
Briefly, how does ANCOVA mathematically perform the feat of comparing every IV on the DV in light of the CV?
ANCOVA uses the regression line between IVs on each subject and calculating each predicted score on the DV based on just the covariate, as if they had scored at the mean of ALL participants on the covariate. Everyone’s score on the DV is adjusted AS IF they all scored at the mean on the covariate
The effects of IVs are assessed holding covariates constant (i.e., treating each subject as if they scored at the overall mean for the covariate)
Provides test of significance for the regression of the covariate(s) on the DV ignoring group effects
Two covariate assumptions?
- CV was measured before the onset of treatment
- CV was measured reliably
How do you test for the extra Assumption: Homogeneity of Regression slopes
- Include covariate-by-IV interaction term(s) in the model, as well as main effects
- If these interactions are significant then there is heterogeneity of regression and ANCOVA is inappropriate
- In SPSS, the Model button allows you to specify the model
Note: a “full factorial model” (SPSS default) does not include interactions between covariates and IVs
We always compare the regression output with the anova output
Describe the legitimate use of ANCOVA… the appropriate use
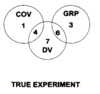
The most appropriate is to remove the effects of noise variables. Best explained by the figures as presented by Miller & Chapman’s Venn Diagrams. For example, 3 groups of subjects might be compared on psychometric tests after being randomly assigned to a particular intervention (training, diet, etc etc). One might know that performance on the tests would be associated with initial IQ score (before randomisation) and so one would to remove the influence of IQ performance. The intention of this approach is to increase the power of the statistical tests for the effects of the experimental variables. THIS USE IS PRIMARILY APPROPRIATE IN EXPERIMENTAL DESIGNS; covariate should be measured before random allocation to groups.
Describe the inappropriate ANCOVA use
Draw the inappropriate ANCOVA use
When groups differ significantly in terms of mean scores for the covariate.
The basic problem is that by using regression methods (in the ANCOVA) to equate all the groups on the covariate(s), one cannot be sure that one is not removing part of the intrinsic difference between the groups, thereby testing an almost meaningless hypothesis about a group variable that doesn’t really reflect the group difference that one wants to test. May illustrate this with 2 Venn diagrams comparing the experimental case (when the group variable will not overlap substantially with the covariate) with other cases in which the covariate and group overlap (ie the groups differ on the covariate). The relationship evaluated by ANCOVA is between the DV and a “group(res)” variable: ie the residual of the group variable after removal of variance shared with the covariate. Such a group variable may be intrinsically different from the group variable that you wanted to assess.
In sum it will usually be inappropriate to use ANCOVA when the groups differ from one another on the covariate (precisely when this use tends, erroneously, to be employed).
Can you describe an illustrative example of the inappropriate use of ANCOVA?
Lord’s Paradox — do boys end up with a higher final weight (DV) after following a specific diet than girls (gender=IV) even when including initial weight as a covariate? part of the intrinsic gender difference is in weight and so using ANCOVA here would end up comparing the weight gain for relatively light boys with the weight gain for relatively heavy girls. This is not the hypothesis we want to test and there are issues about regression to the mean as well (if we sampled light boys at the start of an experiment then they would be likely to have gained more weight than heavy boys – or indeed heavy girls – at a later testing point by regression to the mean).
Miller and Chapman – Imagine using ANCOVA to answer the question would six and eight year old boys differ in weight if they did not differ in height? Once again ANVOVA would create a comparison of short 8 year olds with tall 6 year olds. Do we want to ask that question?
What is an ideal situation for ANCOVA?
- Ideal is small number of orthogonal covariates, each correlated with the DV
- This gives maximum adjustment of the DV for minimum reduction in df for the error term (each covariate reduces error df by 1) – every covariate put in takes 1df away from error term – so harder to become significant, diminishing return as critical F ratio gets larger. Rule of thumb never more than 3.
Name all 4 factors involved with choosing a CV
1) Most variance least CV’s - Goal Maximum adjustment of the DV with minimum loss of degrees of freedom
1) CV must be independent of treatment
2) Data on CVs be gathered before treatment started
3) CV should be reliable (i.e. CV measurement is not much contaminated by noise since measurement noise distorts the resulting effects and it is very problematic for small sample sizes)
What is the problem with non-random assignment ?
It has to do with the intrinsic value thing
In random assignment (experimental) designs, group differences in covariate will be due to chance (as long as covariates measured before assignment)
With nonrandom assignment (common in psychology) covariate differences across groups may reflect meaningful substantive differences related to group membership
ALL PSYCHOLOGY EXPERIMENTS ARE BASICALLY QUASI-EXPERIMENTS
TAKE HOME MESSAGE: YOU CAN’T USE ANCOVA TO MAKE A STATISTIC ‘CORRECTION’ FOR NUISANCE DIFFERENCES BETWEEN YOUR NON-RANDOMLY ASSIGNED GROUPS – BECUS IT DOESN’T WORK, AND CONCEPTUALLY IT DOES THE WRONG THING.
COVARIATION BETWEEN GROUPS MAY WELL REFLECT INTRINISC DIFFERENCES BETWEEN THE GROUPS = WEAKENING EFFECT, BUT EVEN WHEN NOT IT INTRINCIALLY CHANGES THE NATURE OF THE GROUP
Discuss the scenario in detail with respect to the use of the covariate within an analysis of covariance (ANCOVA). Consider what the researchers might be wanting to achieve by including the covariate and whether the analysis would be likely to lead to interpretable findings. Illustrate your answers with examples of other research designs and questions that further illustrate the issues.
Matthew measured performance on a verbal and a spatial memory test and was interested in whether there was a greater gender difference on one kind of memory test than the other. He knew that memory test performance is generally influenced by fluid IQ and so wanted to included an IQ measure as a covariate. The mean IQ of the men and the women in his sample was not significantly different (p>0.3).
This is (almost) the scenario for which ANCOVA works well. That is, using it is an attempt to increase the power of analyses by removing part of the DV variance that is explained by the covariate, so that the IV’s effect on the residual DV variance is proportionally greater and thus more likely to be significant (if an effect exists). Here IQ is known, on the basis of previous research, to explains significant variance in verbal and spatial memory performance, so if IQ variance in these DVs is removed by the ANCOVA procedure, then any effect of gender should be more powerfully revealed. This assumes a reasonable sample size so that the loss of 1 df (for the covariate) isn’t too serious. There is no problem with an IQ difference between men and women that might potentially complicate the analyses.
There is one extra subtlety here (worth 1.5 of the marks). The design sounds as if Matthew measured the verbal and spatial memory within-Ss, although this is confirmed only by the later printout. Matthew is interested in whether gender has a bigger effect on one type of memory test than another, i.e. he is looking for an interaction between gender and test-type. This is mathematically equivalent to a between-Ss test (ANOVA or t) on the memory test difference score. So, for ANCOVA to work well in terms of increasing power in this eg IQ should correlate with the memory test difference score (which is unknown). Thus, we know that using IQ as a covariate will increase the power to detect male-female differences in memory in general (the main effect of gender, which is of less interest), while we have no real expectation that it will increase the power of the interaction (which is of primary interest).
