Motion up to level 6 Flashcards
(26 cards)
Explain the difference between a scalar and a vector
A scalar only has magnitude (size)
A vector is a quantity that has both magnitude and direction
What is the differnce between displacment and distance
Distance is how far you have moved, it is a scalar
Displacment is how far you have moved in a certain direction, it is a vector
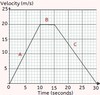
Explain what is shown by the gradient of a distance-time graph
Use the gradient to describe the motion of each of the parts of the graph
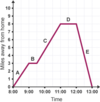
The gradient of a distance time graph tells you the speed that the object is travelling at. A curved line (changing gradient) means that something is accelerating or decelerating.
A: Travelling at a constant speed of 3 mph
B: stationary for half an hour
C: Travelling at a constant speed of 3.3 mph
D: Stationary for one hour
E: returning back to the start at a constant speed of 8mph

What are the typical speeds of:
a) a walker
b) a runner
c) a cyclist
a) 1.5 m/s
b) 3 m/s
c) 6 m/s
What is the equation for speed:
Example calculation: what distance will something travel if it travels at 12m/s for 2 minutes?
Speed can be found from this equation:
Speed = distance/time
speed is measured in meters per second (m/s)
distance is measured in meters (m)
time is measured in seconds (s)
Example calculation:
- convert minutes to seconds. 2 minutes = 120 seconds
- use the formula distance = speed x time to find the answer
12 x 120 = 1440 m
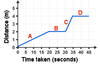
During which section of this journey does the cyclist travel at the fastest speed. Explain how you know this
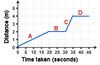
The cyclist travels fasted in section C. This is becuase it has the steepest gradient.
What is the difference between speed and velocity?
Speed is a scalar, it just has magnitude (size)
Velocity is a vector, it has both size and direction.
For example, 10 m/s is a scalar, while 10 m/s north is a vector.
What is the equation that links speed and acceleration?
Example calculation: a car accelerates from 5m/s to 15m/s in 4 seconds, what is its acceleration?
Acceleration can be found from this formula:
Acceleration = change of speed/time
Acceleration is measured in meters per second squared (m/s2)
Speed is measured in meters per second (m/s)
time is measured in seconds (s)
Example calculation:
- calculate the change of speed
change of speed = 15-5 = 10m/s
- use the formula to find the answer
acceleration = change of speed/time
= 10/4
2.5 m/s2
Define the term acceleration
what is its unit?
Acceleration is the rate of change of velocity. This means that it is how quickly you are speeding up or slowing down.
Acceleration is measured in meters per second squared (m/s2)
If a car is moving at a speed of 14m/s and accelerates at a rate of 3m/s for 2 seconds, what is the final velocity of the car?
- Calculate the change of speed using the acceleration equation
change of speed = acceleration x time
= 3 x 2
= 6 m/s
- caculate the final speed
final speed = original speed + change of speed
= 14 + 6 = 20 m/s
NOTE: when using the accleration calculation remember that it gives the change of speed, not the original or final speed
What is given by each of these features of a velocity time graph:
- The gradient
- The area under the graph
Explain how you find the area under the graph
- The gradient of a velocity time graph gives the acceleration of the object.
if there is a positive gradient then the object is speeding up. if there is a negative gradient then the object is slowing down.
- The area under the graph tells you the total distance that the object has travelled
You find the area under the graph by working out the area of one square and then counting the number of squares under the line on the graph. count squares with a diagonal line through them as a half square.
Which of the objects on this velocity time graph is:
- moving at a constant speed
- decelerating
- accelerating the fastest
For each one explain why this is the case
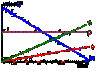
- C is moving at a constant speed. This is seen becuase it is a horizontal line. It has a gradient of 0 so an acceleration of 0.
- A is deccelerating, this can be seen becuase the line is sloping downwards (negative gradient)
- B is accelerating the fastest. This can be seed because it has a positive gradient which is greater than the gradient of D
What is the total distance that the object travels in this velocity time graph. Explain how you find your answer.
- Find the area of one square by multiplying the velocity scale by the time scale.
in this example the time for one large square is 1 second and the velocity for one large square is 10m/s. This makes the area 10m
- count the number of squares and multiply them by the area of eac square.
there are 5 squares and each square has an area of 10m. This means that the total distance travelled is
distance = 5 x 10 = 50m

Explain how to calculate the acceleration of an object that is rolling down a ramp.
- Set up the equipment as shown in the diagram
- set the datalogger to log the velocity of the object and let it roll down the slope
- Plot a graph of velocity against time and find the gradient, this is the acceleration
- Repeat the experiment 3 times and take an average of the gradient. This is done to reduce the effect of random error such as friction in the whee axles and increases the accuracy of the experiment.

Explain how to calculate the speed of the object in this graph
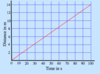
To calculate the speed of an object in a distance time graph you need to take the gradient of the graph.
To do this you pick two points on the graph and measure the change on the y axis between these two points and the change of the x axis between these two point. You then use the formula:
gradient = change of y/change of x
in this example the change of y is from 14 (0-14) and the change of x is 100 (0-100). This means the speed is:
14/100 = 0.14m/s
How do you find the acceleration of an object that is accelerating on a distance time graph?
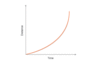
To find the acceleration you draw a tangent, which is a line which touches the curve in only one place.
Then you find the gradient of the tangent and this is the speed of the object.
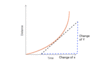
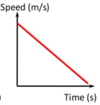
What does this graph show?
This is an object that is accelerating
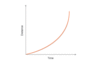
What does this graph show?

This is an object that is deccelerating (slowing down)
What does this graph show?

Something travelling at a constant speed away from the start point
What does this graph show?

Something moving back towards the start point at a constant speed
What does this graph show?
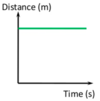
An object that is stationary (not moving)
What does this graph show?
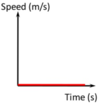
An object that is stationary (not moving)
What does this graph show?
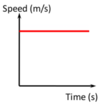
Something moving at a constant speed
What does this graph show?
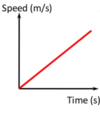
Something that is accelerating