Module 2 – Sampling and Estimation Flashcards
Biased or Unbiased?
DO YOU SUPPORT CHANGING THE LAWS TO PREVENT PEOPLE FROM MAKING THEMSELVES AND OTHERS SICK BY SMOKING IN PUBLIC PLACES?
Biased
Biased or Unbiased?
WHO DO YOU PLAN TO VOTE FOR IN THE NEXT PRESIDENTIAL ELECTION?
Unbiased
Biased or Unbiased?
ARE YOU ONE OF THOSE ANNOYING PEOPLE WHO LIKES POP SINGERS LIKE TAYLOR SWIFT?
Biased
Biased or Unbiased?
HOW MUCH WOULD YOU BE WILLING TO PAY FOR A NEW CAR?
Unbiased
Biased or Unbiased?
HOW MANY TIMES A WEEK DO YOU EAT RED MEAT FOR DINNER?
Unbiased
If a particular standardized test has a mean score of 500 and standard deviation of 100, what percentage of test-takers score between 500 and 600?
- 95%
- 68%
- 34%
- 50%
34%
100 is one standard deviation above the mean (600-500 =100= 1*100 = 1*stdev). We know that approximately 68% of the distribution is within 1 standard deviation of the mean. Therefore 34% must fall beyond 1 standard deviation above the mean.
To better assess student understanding of confidence intervals, a professor gives a test to a random sample of 15 students. The grades for those students are provided below. Calculate the 90% confidence interval for the true average grade on the text.
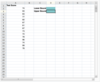
First, calculate the mean and standard deviation of the sample grades using formulas =AVERAGE(A2:A16) and =STDEV.S(A2:A16) in any of the open cells. The values are approximately 76.93 and 11.73 respectively.
Second, calculate the margin of error. Because the sample size is less than 30, use the function CONFIDENCE.T(alpha, standard_dev, size) to find the margin of error using the t-distribution. Here, alpha is 0.1 and the sample size is 15. For the standard deviation value, you need to reference the cell in which you calculated the standard deviation. The result is approximately =CONFIDENCE.T(0.1,11.73,15) = 5.34.
Alternatively, you could use the Descriptive Statistics tool to calculate the mean, standard deviation, and margin of error. To include the margin of error calculation to the Descriptive Statistics output, check the “Confidence Interval” box and adjust the confidence level to 90%. Note that the Descriptive Statistics tool uses CONFIDENCE.T by default to calculate the margin of error.
The lower bound of the 90% confidence interval is the mean minus the margin of error, approximately 76.93–5.34=71.60. The upper bound of the 90% confidence interval is the mean plus the margin of error, approximately 76.93+5.34=82.27. You must link directly to cells in all of your calculations in order to obtain the correct answer.
You can also use a single formula to complete each of the calculations: =AVERAGE(A2:A16)-CONFIDENCE.T(0.1, STDEV.S(A2:A16),15) for the lower bound, and =AVERAGE(A2:A16)+CONFIDENCE.T(0.1, STDEV.S(A2:A16),15) for the upper bound.
For a normal distribution with mean 100 and standard deviation 10, find the probability of obtaining a value less than or equal to 118.
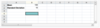
The cumulative probability associated with the value 118 is NORM.DIST(118,B1,B2,TRUE)=0.96, or 96%. Approximately 96% of the population has values less than or equal to 118. Note that because the normal distribution is continuous, the probability of an outcome being equal to single, discrete value (such as 118) is 0. Thus the probability of obtaining a value less than 118 is equivalent to obtaining a value less than or equal to 118. You must link directly to cells to obtain the correct answer.
For a normal distribution with mean 425 and standard deviation 50, find the value associated with the cumulative probability of 25%.
We use the NORM.INV function to find values at cumulative probabilities. Since NORM.INV(0.25,B1,B2)=391, 391 is the value that corresponds to a cumulative probability of approximately 25%. That is, 391 is the 25th percentile of this distribution. You must link directly to cells to obtain the correct answer.
Calculate the 90% confidence interval for the true population mean based on a sample with x¯x¯=15, s=2, and n=20.
Because our sample has fewer than 30 cases, we cannot assume that the distribution of sample means will be normal, and must use the t-distribution. The margin of error is based on the significance level (1-confidence level, or 1-0.90=0.10), the standard deviation (in B2) and the sample size (in B3), and We can compute the margin of error using the Excel function CONFIDENCE.T(0.10,B2,B3). The lower bound of the 90% confidence interval is the sample mean minus the margin of error, that is B1–CONFIDENCE.T(0.10,B2,B3)=15-0.77=14.23. The upper bound of the 90% confidence interval is the sample mean plus the margin of error, that is B1+CONFIDENCE.T(0.10,B2,B3)= 15+0.77=15.77. You must link directly to cells to obtain the correct answer.
For a standard normal distribution, find the probability of obtaining a value less than z=1.5
Recall that the mean of the standard normal distribution is 0 and the standard deviation is 1. Because we know the z-value, we can use the NORM.S.DIST function, which assumes the standardized distribution. NORM.S.DIST(1.5,TRUE)=0.93 or 93%. Alternatively, we can use the NORM.DIST function and explicitly give the mean and standard deviation as 0 and 1 respectively: NORM.DIST(1.5,0,1,TRUE)=0.93, or 93%. 93% of the population is less than z=1.5.
Biased or Unbiased?
WHAT IS YOUR FAVORITE SEASON?
Unbiased
Biased or Unbiased?
HOW MANY TELEVISIONS ARE IN YOUR HOME?
Unbiased
Biased or Unbiased?
WHAT DO YOU THINK CAUSES POLITICIANS TO BE SO NASTY TO ONE ANOTHER?
Biased
Biased or Unbiased?
HOW MUCH MORE IMPORTANT IS LOCATION THAN PRICE WHEN PURCHASING A HOUSE?
Biased
Biased or Unbiased?
DO YOU THINK THAT WE SHOULD ELIMINATE UNEMPLOYMENT INSURANCE SO PEOPLE WILL BE MOTIVATED TO GET A JOB?
Biased
For a normal distribution with mean 425 and standard deviation 50, find the probability of obtaining a value greater than 365.
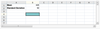
First find the cumulative probability associated with the value 365 using the function NORM.DIST(365,B1,B2,TRUE) = 12%; this is the percentage of cases with values less than 365. To find the percentage of cases with values greater than 365, subtract the cumulative probability of 365 from 100%. 100% – NORM.DIST(365,B1,B2,TRUE)=100% - 12% = 88%. Approximately 88% of the population is greater than 365. You must link directly to cells to obtain the correct answer.
If the average IQ is 100 and the standard deviation is 15, approximately what percentage of people have IQs above 130?
- 10%
- 2.5%
- 5%
- 50%
2.5%
130 is two standard deviations above the mean (130-100=30=2*15=2*stdev). We know that approximately 95% of the distribution is within 2 standard deviations of the mean. Therefore 5% must fall beyond 2 standard deviations, 2.5% at the top and 2.5% at the bottom.
Calculate the 80% confidence interval for the true population mean based on a sample with x¯x¯=225, s=8.5, and n=45.
The margin of error is based on the significance level (1-confidence level, in this case, 100%-80%=20%), the standard deviation (in cell B2) and the sample size (in cell B3). We can compute the margin of error using the Excel function CONFIDENCE.NORM(0.20,B2,B3)=1.62. The lower bound of the 80% confidence interval is the sample mean minus the margin of error, that is B1–CONFIDENCE.NORM(0.20,B2,B3)=225-1.62=223.38. The upper bound of the 80% confidence interval is the sample mean plus the margin of error, that is B1+CONFIDENCE.NORM(0.20,B2,B3)= 225+1.62=226.62. You must link directly to cells to obtain the correct answer.
For a normal distribution with mean 47 and standard deviation 6, find the value associated with the top 10% of outcomes.
To solve problems like this, we can think in terms of cumulative probabilities and use the NORM.INV function. The value associated with the top 10% is the same as the value corresponding to the bottom 90%, so we need to find the value associated with a cumulative probability of 90%. Using NORM.INV(0.90,B1,B2)=55, we find that 90% of the distribution’s values are less than 55; thus 10% of the distribution’s values are greater than 55. If we wish, instead of first computing 100%–10%=90%, we can embed that formula in the function using NORM.INV(1–0.10,B1,B2)=55. You must link directly to cells to obtain the correct answer.
Calculate the 90% confidence interval for the true population mean based on a sample with x¯x¯=225, s=8.5, and n=10.
Because our sample has fewer than 30 cases, we cannot assume that the distribution of sample means will be normal, and must use the t-distribution. The margin of error is based on the significance level (1-confidence level, or 1-0.90=0.10), the standard deviation (in B2) and the sample size (in B3). We can compute the margin of error using the Excel function CONFIDENCE.T(0.10,B2,B3) and it is approximately 4.93. The lower bound of the 90% confidence interval is the sample mean minus the margin of error, that is B1–CONFIDENCE.T(0.10,B2,B3)=225-4.93=220.07. The upper bound of the 90% confidence interval is the sample mean plus the margin of error, that is B1+CONFIDENCE.T(0.10,B2,B3)= 225+4.93=229.93. You must link directly to cells to obtain the correct answer.
Biased or Unbiased?
WHY IS AIR TRAVEL GETTING MORE AND MORE UNPLEASANT?
Biased
Biased or Unbiased?
ABOUT HOW MANY MEALS A WEEK DO YOU EAT AT HOME?
Unbiased
Biased or Unbiased?
ARE YOU INTELLIGENT ENOUGH TO ENJOY THE WORKS OF WILLIAM SHAKESPEARE?
Biased
For a normal distribution with mean 100 and standard deviation 10, find the probability of obtaining a value greater than 70 but less than 80.
First find the cumulative probability associated with the value 80 using the function NORM.DIST(80,B1,B2,TRUE) = 2.275%; this is the percentage of outcomes with values less than 80. Then calculate the cumulative probability 70 using the function NORM.DIST(70,B1,B2,TRUE)=0.01375%; this is the percentage of cases with values less than 70. Then find the difference between the two: NORM.DIST(80,B1,B2,TRUE)–NORM.DIST(70,B1,B2,TRUE)=0.02275-0.00135=0.02140, or 2.140%. 2.140% of the population has values between 70 and 80. You must link directly to cells to obtain the correct answer.
Calculate the 99% confidence interval for the true population mean for the BMI data. Recall that the new sample contains 15 people and has a mean of 25.97 kg/m2 and a standard deviation of 7.10 kg/m2.
Because our sample has fewer than 30 cases, we cannot assume that the distribution of sample means will be normal, and must use the t-distribution. The margin of error is based on the significance level (1-confidence level, or 1-0.99=0.01), the standard deviation (in B2) and the sample size (in B3). We can compute the margin of error using the Excel function CONFIDENCE.T(0.01,B2,B3). The lower bound of the 99% confidence interval is the sample mean minus the margin of error, that is B1–CONFIDENCE.T(0.01,B2,B3)= 25.97-5.46=20.51. The upper bound of the 99% confidence interval is the sample mean plus the margin of error, that is B1+CONFIDENCE.T(0.01,B2,B3)= 25.97+5.46=31.43. We can be 99% confident that the true mean BMI of all U.S. citizens is between 20.51 kg/m2 and 31.43 kg/m2. You must link directly to cells to obtain the correct answer.
For a normal distribution with mean 425 and standard deviation 50, find the value associated with the top 30%.
The value associated with the top 30% is the same as the value corresponding to the bottom 70%, so we need to find the value associated with a cumulative probability of 70%. Using NORM.INV(0.70,B1,B2)=451, we find that 70% of the distribution’s values are less than 451. Thus, 30% of the distribution’s values are greater than 451. If we wish, instead of first computing 100%–30%=70%, we can embed that formula in the function using NORM.INV(1–0.30,B1,B2)=451. You must link directly to cells to obtain the correct answer.
For a normal distribution with mean 47 and standard deviation 6, find the upper value and lower value of the range of outcomes associated with the middle 25%.
Because the normal curve is symmetrical, the middle 25% corresponds to the 12.5% range below the mean and the 12.5% range above the mean. Thus we need to find the cumulative probabilities associated with 50%–12.5%=37.5% and with 50+12.5%=62.5%. Since NORM.INV(0.375,B1,B2)=45 and NORM.INV(0.625,B1,B2)=49, the middle 25% of the probability lies between 45 and 49. Note that these values define a symmetric range centered at the mean. You must link directly to cells to obtain the correct answer.
Calculate the 90% confidence interval for the true population mean based on a sample with x¯x¯=15, s=2, and n=100.
You can separate the calculations into separate formulas or you can combine them into one calculation. The margin of error is based on the significance level (1-confidence level, or 1-0.90=0.1), the standard deviation (in B2), and the sample size (in B3). We can compute the margin of error using the Excel function CONFIDENCE.NORM(0.10,B2,B3). The lower bound of the 90% confidence interval is the sample mean minus the margin of error, that is B1–CONFIDENCE.NORM(0.10,B2,B3)=14.67. The upper bound of the 90% confidence interval is the sample mean plus the margin of error, that is B1+CONFIDENCE.NORM(0.10,B2,B3)=15.33. You must link directly to cells to obtain the correct answer.
For a normal distribution with mean 47 and standard deviation 6, find the probability of obtaining a value less than 45 or greater than 49.
First find the cumulative probability associated with the value 45 using the function NORM.DIST(45,B1,B2,TRUE)=37%; this returns the percentage of outcomes with values less than 45. Then find the percentage of outcomes with values greater than 49 by subtracting the cumulative probability associated with the value 49 from 100% using the function 100% – NORM.DIST(49,B1,B2,TRUE) = 100% – 63% = 37%. Then add the two together: NORM.DIST(45,B1,B2,TRUE)+1–NORM.DIST(49,B1,B2,TRUE)= 37% + 37% = 74%. 74% of the population is less than 45 or greater than 49. You must link directly to cells to obtain the correct answer.
Calculate the 95% confidence interval for the true population mean based on a sample with x¯x¯=15, s=2, and n=100.
The margin of error is based on the significance level (1-confidence level, or 1-0.95=0.05), the standard deviation (in B2) and the sample size (in B3). We can compute the margin of error using the Excel function CONFIDENCE.NORM(0.05,B2,B3). The lower bound of the 95% confidence interval is the sample mean minus the margin of error, that is B1–CONFIDENCE.NORM(0.05,B2,B3)=15-0.39=14.61. The upper bound of the 95% confidence interval is the sample mean plus the margin of error, that is B1+CONFIDENCE.NORM(0.05,B2,B3)=15+0.39=15.39. You must link directly to cells to obtain the correct answer.
Several probability expressions for a normal distribution are provided below. Drag the correct percentage to each probability expression.
Approximately 68% of values are within one standard deviation of the mean. That is, P(μ–σ≤x≤μ+σ)=68%P(μ–σ≤x≤μ+σ)=68%.
Approximately 95% of values are within two standard deviations of the mean, so 95%2=47.5%95%2=47.5% of values are between two standard deviations below the mean and mean. That is, P(μ–2σ≤x≤μ)=47.5%P(μ–2σ≤x≤μ)=47.5%.
Approximately 68% of values are within one standard deviation of the mean, so 68%2=34%68%2=34% of values are between one standard below the mean and the mean. That is, P(μ–σ≤x≤μ)=34%P(μ–σ≤x≤μ)=34%. Since P(μ–2σ≤x≤μ)=47.5%P(μ–2σ≤x≤μ)=47.5%, P(μ–2σ≤x≤μ–σ)=P(μ–2σ≤x≤μ)–P(μ–σ≤x≤μ)=47.5%–34%=13.5%P(μ–2σ≤x≤μ–σ)=P(μ–2σ≤x≤μ)–P(μ–σ≤x≤μ)=47.5%–34%=13.5% of values are between two standard deviations below the mean and one standard deviation below the mean.
Approximately 95% of values are within two standard deviations of the mean, so 5% of values are outside of that range. Thus, 5%2=2.5%5%2=2.5% are greater than or equal to two standard deviations above the mean. That is, P(μ+2σ≤x)=2.5%P(μ+2σ≤x)=2.5%.
If the mean of a normally distributed population is -10 with a standard deviation of 2, what is the likelihood of obtaining a value less than or equal to -7?
To calculate the likelihood of obtaining a value less than or equal to -7, P(x≤-7), use the Excel function NORM.DIST(x, mean, standard_dev, TRUE). Here, NORM.DIST(-7,B1,B2,TRUE)=NORM.DIST(-7,-10,2,TRUE)=0.93, or 93%. Approximately 93% of the population falls in the area under the curve less than or equal to -7.
A store owner is interested in opening a second shop. She wants to estimate the true average daily revenue of her current shop to decide whether expanding her business is a good idea. The store owner takes a random sample of 60 days over a six-month period and finds that the mean revenue of those days is 3,472.00 dollars with variance 315,900.20 square dollars. Calculate a 95% confidence interval to estimate the true average daily revenue.
First calculate the sample standard deviation, which is equal to the square root of the variance. The sample standard deviation is $562.05. Then find the margin of error using the Excel function CONFIDENCE.NORM(alpha, standard_dev, size). Here, CONFIDENCE.NORM(0.05,SQRT(B2),60)=CONFIDENCE.NORM(0.05,562.05,60)=$142.22. The lower bound of the 95% confidence interval is the mean minus the margin of error, $3,472.00–$142.22=$3,329.78. The upper bound of the 95% confidence interval is the mean plus the margin of error, $3,472.00+$142.22=$3,614.22. You must link directly to values in order to obtain the correct answer.
A curious student in a large economics course is interested in calculating the percentage of his classmates who scored lower than he did on the GMAT; he scored 490. He knows that GMAT scores are normally distributed and that the average score is approximately 540. He also knows that 95% of his classmates scored between 400 and 680. Based on this information, calculate the percentage of his classmates who scored lower than he did.
Since GMAT scores are normally distributed, we know that P(μ–1.96σ ≤ x ≤ μ+1.96σ) = 95%. Thus, to find the standard deviation, subtract the lower bound from the mean and divide by 1.96. The standard deviation of the distribution is (B1-B2)/1.96 = (540-400)/1.96 = 71.4. (Note that because the normal curve is symmetrical, we could calculate the same value using (B3-B1)/1.96 = (680-540)/1.96 = 71.4). To find the cumulative probability, P(x ≤ 490), use the Excel function NORM.DIST(x, mean, standard_dev, TRUE). Here, NORM.DIST(B4,B1,71.4,TRUE) = NORM.DIST(490,540,71.4,TRUE) = 0.24, or 24%. Approximately 24% of his classmates scored lower than he did. You must link directly to the values in order to obtain the correct answer
A researcher wants to select a random sample of consumers for a study. Generate a random ID number between 0 and 1,000 for each consumer in the spreadsheet.
Use the function =RAND()*1000 in cells A2:A30 to generate random numbers for each consumer.
A journalist wants to determine the average annual salary of CEOs in the S&P 1,500. He does not have time to survey all 1,500 CEOs but wants to be 95% confident that his estimate is within $50,000 of the true mean. The journalist takes a preliminary sample and estimates that the standard deviation is approximately $449,300. What is the minimum number of CEOs that the journalist must survey to be within $50,000 of the true average annual salary? Remember that the z-value associated with a 95% confidence interval is 1.96.
Please enter your answer as an integer; that is, as a whole number with no decimal point.
Number:
The formula for calculating the minimum required sample size is n≥(zsM)2n≥(zsM)2, where M=50.000 is the desired margin of error for the confidence interval, s=$449,300 is the sample standard deviation, and z=1.96.
Using these data we find that 1.96449,30050,0002=310.201.96449,30050,0002=310.20 Since n must be an integer (let’s not even think of what 0.20 CEOs would look like!) and n must be greater than or equal to 310.20, we must round up to 311. Since 310.20 is closer to 310 than to 311, we would normally round 310.20 down to 310. However, in this case we must round up to find the smallest integer that satisfies the equation. Therefore, the minimum required sample size is 311.
A college student is interested in investigating the TV-watching habits of her classmates and surveys 20 people on the number of hours they watch per week. The results are provided below. Calculate the 80% confidence interval of the true average number of hours of TV watched per week.
First calculate the mean and standard deviation of the sample, which you can do in Excel using either the descriptive statistics tool or the AVERAGE and STDEV.S functions. The mean and standard deviation are approximately 9.65 and 4.61 hours respectively. Since the sample size is only 20, use the function CONFIDENCE.T(alpha, standard_dev, size) to find the margin of error using the t-distribution. Here, this is approximately CONFIDENCE.T(0.2,4.61,20)=1.37. The lower bound of the 80% confidence interval is the mean minus the margin of error, 9.65–1.37=8.28 hours. The upper bound of the 80% confidence interval is the mean plus the margin of error, 9.65+1.37=11.02 hours. You must link directly to values in order to obtain the correct answer.
A college football coach has decided to recruit only the heaviest 15% of high school football players. He knows that high school players’ weights are normally distributed and that this year, the mean weight is 225 pounds with a standard deviation of 43 pounds. Calculate the weight at which the coach should start recruiting players.
Use the properties of the normal distribution to solve this problem. Since the coach is only interested in recruiting the heaviest 15% of players, calculate the weight that 85% of players weigh less than. The Excel function NORM.INV(probability, mean, standard_dev) returns the inverse of a normal cumulative distribution function. Here, NORM.INV(0.85,B1,B2)=NORM.INV(0.85,225,43)=269.57 indicates that 85% of players weigh less than 268.95 pounds. Hence, 15% of high school players weigh 269.57 pounds or more.
A company randomly surveys 15 VIP customers and records their customer satisfaction scores out of a possible 100 points. Based on the data provided, calculate a 90% confidence interval to estimate the true satisfaction score of all VIP customers.
First calculate the mean and standard deviation of the sample, which you can do in Excel using either the descriptive statistics tool or the AVERAGE and STDEV.S functions. The mean and standard deviation are approximately 76.60 and 11.28 respectively. Since the sample size is only 15, use the function CONFIDENCE.T(alpha, standard_dev, size) to find the margin of error using the t-distribution. Here, this is approximately CONFIDENCE.T(0.1,11.28,15)=5.13. The lower bound of the 90% confidence interval is the mean minus the margin of error, 76.60–5.13=71.47. The upper bound of the 90% confidence interval is the mean plus the margin of error, 76.60+5.13=81.73. You must link directly to values in order to obtain the correct answer.
IQ scores are known to be normally distributed. The mean IQ score is 100 and the standard deviation is 15. What percent of the population has an IQ over 115?
To find P(x>115), the percent of the population has an IQ over 115, first compute the cumulative probability, P(x≤115), using the Excel function NORM.DIST(x, mean, standard_dev, TRUE). Here NORM.DIST(115,B1,B2,TRUE)=NORM.DIST(115,100,15,TRUE)=0.84, or 84%. Thus, P(x>115)=1–P(x≤115)=1–0.84=0.16, or 16%.
IQ scores are known to be normally distributed. The mean IQ score is 100 and the standard deviation is 15. What percent of the population has an IQ between 85 and 105?
To find P(85≤x≤105), the percent of the population has an IQ between 85 and 105, first compute the cumulative probability, P(x≤105), using the Excel function NORM.DIST(x, mean, standard_dev, TRUE). Then subtract the cumulative probability P(x≤85). Here NORM.DIST(105,B1,B2,TRUE)–NORM.DIST(85,B1,B2,TRUE)=NORM.DIST(105,100,15,TRUE)–NORM.DIST(85,100,15,TRUE)=0.61–0.16=0.47, or 47%. Approximately 47% of people have IQ scores between 85 and 105.
IQ scores are known to be normally distributed. The mean IQ score is 100 and the standard deviation is 15. The top 25% of the population (ranked by IQ score) have IQ’s above what value?
Use the properties of the normal distribution to solve this problem. Since you are only interested in the top 25%, calculate the IQ at which 75% of people are below. The Excel function NORM.INV(probability, mean, standard_dev) returns the inverse of a normal cumulative distribution function. Here, NORM.INV(0.75,B1,B2)=NORM.INV(0.75,100,15)=110 indicates that 75% of people have IQ’s lower than 110. Hence, 25% of people have IQ’s greater than 110.
You must use a spreadsheet function to create the dummy variable. Your answer will be graded as incorrect if you manually enter the dummy variable data.
Cells B2:B126 should contain a value of 1 or 0 depending on whether column A indicates that the voter voted for or against the candidate. In cell B2, enter the function =IF(A2=”For”,1,0), then copy and paste this function into cells B3:B126. You must use the IF function and link to cells.
Calculate the 90% confidence interval for the proportion of voters who cast their ballot for the candidate.
The political campaign can be 90% confident that the true population proportion of voters who cast a ballot for the candidate is between 29.7% and 43.9%.
Since the sample size is greater than 30, we can determine the margin of error using the CONFIDENCE.NORM function. The margin of error is CONFIDENCE.NORM(0.10,STDEV.S(B2:B126),125)=0.071, or approximately 7%. The lower bound of the 90% confidence interval is the sample mean minus the margin of error, AVERAGE(B2:B126)–CONFIDENCE.NORM(0.10, STDEV.S(B2:B126),125)=0.368–0.071=0.297, or 29.7%. Similarly, the upper bound of the 90% confidence interval is the sample mean plus the margin of error, AVERAGE(B2:B126)+CONFIDENCE.NORM(0.10, STDEV.S(B2:B126),125)=0.368+0.071=0.439, or 43.9%.
Note that you can alternatively calculate the mean and standard deviation of the sample in adjacent cells (or by using the descriptive statistics tool) and linking to the cell values.
