Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

HBS S > Analytics Final Exam > Flashcards

Analytics Final Exam Flashcards

1
Q

A real estate developer has data on several financial variables for each quarter from 1995 to 2001. The variables are housing starts (in thousands), the housing price index (a measure of average housing selling prices), unemployment rate, average disposable income, and home owner vacancy rates. A partial view of the data set containing the 80 observations is given below.

In order to create a regression model to analyze the relationship between housing starts and the other housing-related and macro-economic variables, which cell references should be entered?

  • Input Y Range: A1:B81 Input X Range: C1:F81
  • Input Y Range: B1:F81 Input X Range: A1:A81
  • Input Y Range: B1:F81 Input X Range: A1:A81
  • Input Y Range: B1:B81 Input X Range: C1:F81
A

​

  • Input Y Range: B1:B81 Input X Range: C1:F81
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Suppose we want to assign dummy variables to the seasons (Winter, Spring, Summer, Fall). How many dummy variables do we need?

  • 1
  • 2
  • 3
  • 4
A

1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

A real estate developer has data on a number of U.S. National financial variables for each quarter from 1995 to 2001. The variables are housing starts (in thousands), the housing price index (a measure of average housing selling prices), unemployment rate, average disposable income, and home owner vacancy rates. A partial view of the data is below.

If the developer wanted to create a regression model to predict housing starts from all the other financial variables, which of the following would be INDEPENDENT variables? (Select all that apply.)

  • Year and Quarter
  • Housing Starts (thousands)
  • House Price Index
  • Unemployment Rate
  • Disposable Income
  • Home Owner Vacancy Rates
A

House Price Index
Unemployment Rate
Disposable Income
Home Owner Vacancy Rates

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

A restaurant supply manager analyzes the relationship between a restaurant’s location and the number of meals consumed by comparing clients in two locations: Munich and Paris. The manager’s first regression model uses the number of meals consumed as the dependent variable and a dummy variable for location (Munich or Paris) as an independent variable. This model has an R-squared of 0.712, and the coefficient for location is statistically significant.

The manager runs a second model, adding another variable, the amount of wine consumed with meal. In this model, the coefficient for location is no longer significant, the R-squared has increased from 0.712 to 0.719, and the adjusted R-squared has decreased. Which of the following is the most likely reason for this pattern of changes?

  • The owner made a mistake; it is impossible for a once significant variable to no longer be significant.
  • The variables for location and wine consumption are collinear.
  • The variable for location is a better predictor than wine consumption.
  • Neither location nor wine consumption is a good predictor in the model.
A

The variables for location and wine consumption are collinear.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

How would you describe the shape of the distribution shown below?

  • Uniform
  • Right-tailed
  • Left-tailed
  • Symmetric
A

Right-tailed

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

How many houses cost more than $200 thousand and less than or equal to $800 thousand?

  • Approximately 11
  • Approximately 15
  • Approximately 22
  • Approximately 25
A

22

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

A manager examines the histogram below and, after conducting additional research, finds that the observation in bin 3 is an input error and should have been entered as 13. If the histogram is updated with the correct number, which of the following will occur?

  • The mean will decrease.
  • The mode will increase.
  • The median will increase.
  • The standard deviation will decrease.
A

The standard deviation will decrease.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

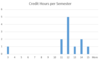
Which of the following Excel formulas or tools would correctly calculate the average hourly hot dog sales over a two-day period from the data shown below? SELECT ALL THAT APPLY.

  • The Descriptive Statistics tool
  • AVERAGE(B2:B17)
  • AVERAGEIF(B2:B17)
  • MEAN(B2:B17)
  • MEDIAN(B2:B17)
  • MODE.SNGL(B2:B17)
  • SUM(B2:B17)/COUNT(B2:B17)
A
  • The Descriptive Statistics tool
  • AVERAGE(B2:B17)
  • SUM(B2:B17)/COUNT(B2:B17)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

If the variance of a data set is 486.75, what is the standard deviation?

Please give your answer rounded to 2 digits to the right of the decimal point. That is, if you think the answer is 486.750101, you should enter 486.75. [Fill in the blank]

[Blank]

A

22.06

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

The scatterplot below shows the temperature and the amount of hot chocolate sold for sixteen randomly selected days in a coffee shop in Boston. What is the most likely correlation between temperature and hot chocolate sold?

  • -.8
  • -.2
  • .2
  • .8
A

-.8

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

The spreadsheet below contains data for 30 students’ grades and the number of hours each student spent studying. What formula would give the correlation between hours studying and quiz grades?

  • CORREL(A1:A30, B1:B30)
  • CORREL(A1,A30, B1,B30)
  • CORREL(A2:A31, B2:B31)
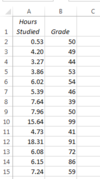
  • CORREL(A2,A31, B2,B31)
A

CORREL(A2:A31, B2:B31)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

A real estate firm wants to calculate percentiles for the prices of 25 houses it has listed. If the prices are listed in cells A2:A26, which of the following Excel functions would calculate the 95th percentile?

  • PERCENTILE.INC(A2:A26,0.05)
  • PERCENTILE.INC(A2:A26,0.95)
  • PERCENTILE.INC(A2:A26,0.025)
  • PERCENTILE.INC(A2:A26,0.975)
A

PERCENTILE.INC(A2:A26,0.95)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

The scatter plot below shows the home sales of an independent real estate broker over several years. Approximately how many more homes did the broker sell in 2014 than in 2012?

  • 5
  • 10
  • 15
  • 20
A

10

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Which of the following questions are biased? SELECT ALL THAT APPLY.

  • How much more important is location than price when purchasing a house?
  • What is your favorite season of the year?
  • Do you think that we should eliminate unemployment insurance so people will be motivated to get a job?
  • What do you think causes politicians to be so nasty to one another?
  • How many televisions are in your home?
A
  • How much more important is location than price when purchasing a house?
  • Do you think that we should eliminate unemployment insurance so people will be motivated to get a job?
  • What do you think causes politicians to be so nasty to one another?
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

For a sample with x¯x¯ =15, s=2, and n=25, which of the following formula would calculate the upper bound of the 95% confidence interval for the true population mean? Please note that the Excel functions for confidence intervals are CONFIDENCE.NORM(alpha, standard_dev, size) and CONFIDENCE.T(alpha, standard_dev, size).

  • =15+CONFIDENCE.T(0.05,2,25)
  • =15+CONFIDENCE.T(0.025,2,25)
  • =15+CONFIDENCE.NORM(0.05,2,25)
  • =15+CONFIDENCE.NORM(0.025,2,25)
A

=15+CONFIDENCE.T(0.05,2,25)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

A travel agent wants to determine how much the average client is willing to pay for a weekend at an all-expense paid resort. The agent surveys 30 clients and finds that the average willingness to pay is $2,500 with a standard deviation of $840. However, the travel agent is not satisfied and wants to be 95% confident that the sample mean falls within $150 of the true average. What is the minimum number of clients the travel agent should survey? Note that z=1.96 for a 95% confidence interval.

Please give your answer as an integer with no decimal point and no digits to the right of the decimal point.

[BLANK]

A

121

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

A bar owner wants to know if the installation of large-screen TV over the bar has increased the number of drinks sold per hour. Before the TVs were installed, the bar sold an average of 162 drinks per hour. What alternative hypothesis should the manager use to test this claim?

  • µ ≠ 162 drinks
  • µ ≤ 162 drinks
  • µ < 162 drinks
  • µ > 162 drinks
A

µ > 162 drinks

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

A popular hair salon wants to gather data about how returning customers rate the quality of the service they received during their most recent appointment. The owner decides to use a survey to gather this data. What is the BEST option for selecting respondents to the survey?

  • Place paper surveys near the entrance of the hair salon.
  • Randomly select a sample of returning customers from appointment records and mail them a survey.
  • Ask for volunteers among returning customers and conduct in-person surveys with them during their appointment.
  • Conduct a phone survey of all customers who have received blonde highlights in the salon in the last six months.
A

Randomly select a sample of returning customers from appointment records and mail them a survey.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Assuming that all else remains constant, what happens to a confidence interval around the mean if we raise the sample size from 25 to 100?

  • The width of the confidence interval remains the same.
  • The width of the confidence interval widens.
  • The width of the confidence interval narrows.
  • The answer cannot be determined without further information.
A

The width of the confidence interval narrows.

20
Q

The manager of a small bar is trying to decide whether to invest in a large-screen television. The manager leases a television for ten weeks and monitors sales during that period. Before the manager installed the television, average weekly revenue was approximately $27,000. With the television installed, average weekly revenue was approximately $32,000. After performing a hypothesis test, the editor obtained a p-value of 0.04. Assuming a 95% confidence level, which of the following conclusions is correct?

  • Do not reject the null hypothesis, and conclude that the television does not increase revenue.
  • Do not reject the null hypothesis, and conclude that the television increases revenue.
  • Reject the alternative hypothesis, and conclude that the television increases revenue
  • Reject the null hypothesis, and conclude that the television increases revenue.
A

Reject the null hypothesis, and conclude that the television increases revenue.

21
Q

The manager of a factory that is making an average of 14,000 pints of ice cream a day decides to start playing music for employees, believing this decision will increase both employee morale and productivity. However, the manager is concerned about the possibility that the music could distract employees, thereby decreasing productivity. After a month of playing music, the factory was making an average of 13,518 pints a day. The manager runs a two-sided hypothesis test to determine if the number of pints produced has changed. The p-value of the test is 0.238. What does this say about ice cream production?

  • If there were no actual change in the average number of pints of ice cream produced daily, the chance of seeing average ice cream production as low as 13,518 pints would be 23.8%.
  • There is a 76.2% chance that the mean number of pints of ice cream produced daily has changed since the manager started playing music.
  • There is a 76.2% chance that the sample mean number of pints of ice cream produced is 13,518 a day.
  • The manager should expect to produce more than 13,518 pints of ice cream on 23.8% of the days that the factory is running.
A

If there were no actual change in the average number of pints of ice cream produced daily, the chance of seeing average ice cream production as low as 13,518 pints would be 23.8%.

22
Q

If a standardized test has a mean score of 500 and standard deviation of 100, what percentage of test-takers score between 500 and 600?

  • 95%
  • 68%
  • 34%
  • 50%
A

34%

23
Q

The linear relationship between two variables can be statistically significant but not explain a large percentage of the variation between the two variables. This would correspond to which pair of R^2 and p-value?

  • Low R-squared, Low p-value
  • Low R-squared, High p-value
  • High R-squared, Low p-value
  • High R-squared, High p-value
A

Low R-squared, Low p-value

24
Q

A professor wants to know if the average exam score differs between students who attended a review session and those who did not attend. What null hypothesis should the professor use to test this claim?

  • µattended > µdid not attend
  • µattended ≥ µdid not attend
  • µattended ≤ µdid not attend
  • µattended = µdid not attend
A

µattended = µdid not attend

25
Q

The mean score on a particular standardized test is 500, with a standard deviation of 100. To assess whether a training course has been effective in improving scores on the test, we take a random sample of 20 students from the course and find that the average score of this sample is 550. Which function would correctly calculate the 95% range of likely sample means under the null hypothesis?

  • 550 ± CONFIDENCE.NORM(0.05,100,20)
  • 550± CONFIDENCE.T(0.05,100,20)
  • 500 ± CONFIDENCE.T(0.05,100,20)
  • 500 ± CONFIDENCE.NORM(0.05,100,20)
A

500 ± CONFIDENCE.T(0.05,100,20)

26
Q

Use the regression equation below to determine what happens to the average selling price of a house when house size increases by 500 square feet.

SellingPrice=13,490.45+255.36(HouseSize)SellingPrice=13,490.45+255.36(HouseSize), where HouseSizeHouseSize is measured in square feet and SellingPriceSellingPrice is in dollars

  • Average selling price would remain the same
  • Average selling price would increase by approximately $13,490
  • Average selling price would increase by approximately $140,990
  • Average selling price would increase by approximately $127,500
A

Average selling price would increase by approximately $127,500

27
Q

If the two-sided p-value of a given sample mean is 0.0040, what is the one-sided p-value for that sample mean?

  • 0.0020
  • 0.0040
  • 0.0080
  • The answer cannot be determined without further information
A

0.0020

28
Q

The graph below displays the range of historical data for house size (in thousands of square feet) and selling price (in thousands of dollars), along with the associated regression line. For which house size would the forecast for selling price have the lowest expected forecast error?

  • 1,000 square feet
  • 1,500 square feet
  • 4,500 square feet
  • The forecast error would be the same for all of these forecasts
  • The answer cannot be determined without further information.
A

1,500 square feet

29
Q

Given the general regression equation, ŷ =a+bxy^=a+bx, which of the following describes ŷ y^? Select all that apply.

  • The expected value of the dependent variable
  • The expected value of the independent variable
  • The value we are trying to predict
  • The intercept
  • The slope
A
  • The expected value of the dependent variable
  • The value we are trying to predict
30
Q

Which of the following p-values would indicate that we can be 95% confident that there is a significant linear relationship between two variables? Select all that apply.

  • 0.0025
  • 0.0100
  • 0.9500
  • 0.9750
A
  • 0.0025
  • 0.0100
31
Q

When analyzing a residual plot, which of the following indicates that a linear model is a good fit?

  • Patterns or curves in the residuals
  • Increasing size of the residuals as values increase along the x-axis
  • Decreasing size of the residuals as values increase along the x-axis
  • Random spread of residuals around the y-axis
  • Random spread of residuals around the x-axis
A
  • Random spread of residuals around the x-axis
32
Q

Use the regression equation below to predict the selling price of a three-year old popular car model.

CarResaleValue=35,075−2,079.25(Age)CarResaleValue=35,075−2,079.25(Age), where AgeAge is measured in years and CarResaleValueCarResaleValue is in dollars

Enter your answers in the space provided. Please give your answer with 2 digits to the right of the decimal point and do not insert commas or dollar signs. That is, if you think the answer is $3,215.916524, you should enter 3215.92.

[BLANK]

A

28837.25

33
Q

A p-value to test the significance of a linear relationship between two variables was calculated to be 0.0210. What can we conclude? SELECT ALL THAT APPLY.

  • We can be 90% confident that there is a significant linear relationship between the two variables.
  • We can be 95% confident that there is a significant linear relationship between the two variables.
  • We can be 98% confident that there is a significant linear relationship between the two variables.
  • We can be 99% confident that there is a significant linear relationship between the two variables.
A
  • We can be 90% confident that there is a significant linear relationship between the two variables.
  • We can be 95% confident that there is a significant linear relationship between the two variables.
34
Q

Use the regression equation below to predict the selling price of a 3,500 square foot home.

Selling Price=13,490.45+255.36(House Size) Selling Price=13,490.45+255.36(House Size), where HouseSizeHouseSize is measured in square feet and SellingPriceSellingPrice is in dollars

Enter your answers in the space provided. Please give your answer with 2 digits to the right of the decimal point and do not insert commas or dollar signs. That is, if you think the answer is $3,215.916524, you should enter 3215.92.

[BLANK]

A
  • Gender
  • Level of Education (highest degree earned)
35
Q

For each of the following variables, determine if dummy variables should be created for a regression analysis. SELECT ALL THAT APPLY

  • Gender
  • Age (in years)
  • Income (in dollars)
  • Level of Education (highest degree earned)
A

Gender

Level of Education

36
Q

The spreadsheet below contains a partial view of data about U.S. corn acreage planted (in millions of acres) and the amount of corn (in millions of bushels) in storage from the previous year at the beginning of the year for each year from 1976 to 2013.

We wish to use the data to predict the number of acres of corn that will be planted, based on the beginning corn stock in storage. Which variable is the independent variable?

  • Corn Acreage Planted (in million acres)
  • Stock of Corn at Start of Year (in million bushels)
A

Stock of Corn at Start of Year (in million bushels)

37
Q

The owner of an electronics shop creates a regression model to help determine the price of a TV based on the size of its screen (in square inches), the quality of its picture (rated on a scale of 1 to 10 by a panel of judges) and the quality of its sound (also rated on a scale of 1 to 10 by a panel of judges). The regression equation is:

Price=256+1.60(Screen Size)+0.55(Picture Quality)+0.32(Sound Quality)Price=256+1.60(Screen Size)+0.55(Picture Quality)+0.32(Sound Quality)

Which is the dependent variable?

  • Price
  • Screen Size
  • Picture Quality
  • Sound Quality
A

Price

38
Q

The owner of an electronics shop creates a regression model to help determine the price of a TV based on the size of its screen (in square inches), the quality of its picture (rated on a scale of 1 to 10 by a panel of judges) and the quality of its sound (also rated on a scale of 1 to 10 by a panel of judges). The regression equation is:

Price=256+1.60(Screen Size)+0.55(Picture Quality)+0.32(Sound Quality)Price=256+1.60(Screen Size)+0.55(Picture Quality)+0.32(Sound Quality)

What is the coefficient for Picture Quality?

  • 256
  • 1.60
  • 0.55
  • 0.32
A

0.55

39
Q

Below is a regression output table based on data from the 2014 Major League Baseball (MLB) season. The dependent variable is Win Percentage (the percentage of games won by MLB teams) in 2014. The independent variables are as follows: Runs (the average number of runs the team scored per game); ERA (the average number of runs the team allowed the opposing team to score per game); Completed Games (the total number of games with only one pitcher for the entire game); and strikeouts (the total number of strikeouts for the season).

Which of the following independent variables are significant at the p < .05 level?

  • Completed_Games
  • Runs
  • ERA
  • Strikeouts
A

ERA

40
Q

A grocery store owner wants to analyze how weather, day of the week, and time of day are related to the number of transactions completed per hour. Which of the following hypothesis tests is NOT conducted in the multiple regression model that contains these variables?

  • A hypothesis test for the significance of weather on number of transactions completed per hour, provided that day of the week and time of day remain constant
  • A hypothesis test for the significance of day of the week on time of day, provided number of transactions remain constant
  • A hypothesis test for the significance of day of the week on number of transactions completed per hour, provided that time of day and weather remain constant
  • A hypothesis test for the significance of time of day on number of transactions completed per hour, provided that day of the week and weather remain constant
A

A hypothesis test for the significance of day of the week on time of day, provided number of transactions remain constant

41
Q

Below is a residual plot from a model predicting the cost (in cents) of a standard postage stamp from the year the stamp was issued. Do you think the linear model is a good fit for the data?

  • Yes, this looks like a good regression model.
  • No, this looks like a non-linear relationship.
  • No, there is heteroskedasticity.
A

No, this looks like a non-linear relationship.

42
Q

Use the multiple regression model below to predict the selling price of a house that is 3,000 square feet in size and 20 miles from Boston.

Selling Price=194,986.59+244.54(House Size)–10,840.04(Distance from Boston)Selling Price=194,986.59+244.54(House Size)–10,840.04(Distance from Boston), where Selling Price is in dollars, House Size is measured in square feet, and Distance from Boston is in miles

Enter your answer in the space provided. Please give your answer with 2 digits to the right of the decimal point and do not insert commas or dollar signs. That is, if you think the answer is $3,215.916524, you should enter 3215.92.

[BLANK]

A

711805.79

43
Q

Use the multiple regression model below to predict the selling price of a house that is 1,500 square feet in size and 10 miles from Boston.

Selling Price=194,986.59+244.54(House Size)–10,840.04(Distance from Boston) Selling Price=194,986.59+244.54(House Size)–10,840.04(Distance from Boston), where Selling Price is in dollars, House Size is measured in square feet, and Distance from Boston is in miles.

  • $453,396.19
  • $454,087.00
  • $670,196.99
  • $550,096.55
A

$453,396.19

44
Q

Assume we have created two single linear regression models, and a multiple regression model to predict selling price based on HouseSizeHouseSize alone, Distance from Boston alone, or both. The three models are as follows, where House Size is in square feet and Distance from Boston is in miles:

Selling Price=13,490.45+255.36(House Size) Selling Price=13,490.45+255.36(House Size) Selling Price=686,773.86–15,162.92(Distance from Boston) Selling Price=686,773.86–15,162.92(Distance from Boston) Selling Price=194,986.59+244.54(House Size)–10,840.04(Distance from Boston) Selling Price=194,986.59+244.54(House Size)–10,840.04(DistancefromBoston)

House A and House B are the same size, but located in different neighborhoods: House B is five miles closer to Boston than House A. If the selling price of House A is $450,000, what would we expect to be the selling price of House B?

  • Approximately $396,000
  • Approximately $504,000
  • Approximately $526,000
  • Approximately $699,000
  • The answer cannot be determined without further information
A

Approximately $504,000

45
Q

If you are performing a hypothesis test based on a 90% confidence level, what are your chances of making a type I error?

  • 90%
  • 10%
  • 5%
  • It is not possible to tell without more information
A

10%

46
Q
A

HBS S (6 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions