MMB-Stats_1_Science-Means-SD Flashcards
(28 cards)
- What is science and what does “it” do?
List 9 answers.
- Science is an attitude, or a process, not a body of facts.
- It involves learning from mistakes.
- It does not accept the argument from authority.
- Science does not claim to have the complete truth about anything, but aims to improve its approximation to the truth as a result of this process. A clock can still be useful even it it doesn’t keep perfect time; it can be worth striving to improve the accuracy of even a good clock.
- Science involves a constant process of asking questions.
- It seeks for generalisations, but it is valid to map out diversity as well (ie exceptions to the generalisations).
- It collects objective evidence.
- It makes testable statements.
- It adopts a sceptical attitude towards all claims, but remains open-minded about them.
- What is the standard paradigm in science?
- Formulate a hypothesis, based on previous knowledge (model and hypothesis are often used interchangeably)
- design and carry out a study to test it,
- analyse the results
- do they confirm or refute the hypothesis?
- if necessary reformulate the hypothesis in the light of the conclusions.
- Repeat the process.
- What is the gold standard for providing evidence of causality?
The gold standard for providing evidence of causality is the randomised controlled trial.
- What does a randomised controlled trial entail?
- A treatment group and a control group (and sometimes a placebo group as well),
- random allocation of participants to these groups,
- some kind of objective measure as a dependent variable, with an operational definition,
- and usually, statistical analysis of the results, with a difference between groups only accepted if some agreed significance level is exceeded.
- What is an operational definition of a variable?
An operational definition of a variable is a set of activities required to measure that variable. This allows other researchers to check claims made about that variable.
- Discuss **probability **
Probability is often defined by starting with a lot of “equally probable” events (eg dice coming up as 1, 2, 3, etc). In the long run, you would expect 1 to come up 1/6th of the time, 2 to come up 1/6th of the time, and so on. Even numbers will come up (1/6 + 1/6 + 1/6) = ½ of the time. This comprises the frequentist view of probability.
- What is a histogram and what are it’s uses?
A histogram is a graphical display of frequencies.
Equally probable events would give rise to an approximately flat histogram, but in practice histograms of real-life variables such as height, weight or IQ for a population tend to approximate to a normal or Gaussian distribution.
There is a peak at the mean, and it tails off either side. The “shoulders” of the curve (at the points of inflexion where it goes from convex to concave) are at almost exactly one standard deviation either side of the mean.
- What does reliability measure?
Reliability measures the amount of precision in a measurement: high reliability means high precision, which is the same as low random error.
If you made the same measurement on the same individual repeatedly, the random error is the standard deviation of the numbers you would get.
- Give a technical definition of reliability and give an example.
1 – (error variance of a variable/population variance of the variable).
So if eg IQ can be measured with an error standard deviation of 5 points, and it has a population sd of 15 points, the reliability of the measurement is 1 – (5squared/15squared) = 1 – 1/9 = 8/9 = 88.9%.
- When is a measurment valid?
A measurement is valid when it gives outcomes which are on average close to the correct result. So high validity corresponds to low systematic error.
The mean of a set of measurements of an individual is close to the true value for that individual, and this statement is true for all individuals if the measurement is to be valid.
- What are variables and how are they measured in phsycological experiments?
Variables can be:
Categorical (or nominal or non-parametric): where there is no natural allocation of numbers to the levels of the variable (eg religion of an individual, gender, occupation).
Parametric variables, or covariates: these can be ordinal (eg scores on a Likert scale), interval (eg Celsius temperature) or ratio (where there is a well-defined zero).
- What is the difference between populations and samples?
A population is the entire collection of things that you are looking at and that you could theoretically measure: should define the population explicitly. Ideally, your sample is chosen randomly from the population.
A sample is a smaller, hopefully representative subset of the population that you actually measure. This enables you to make inferences about the population itself, which you cannot study directly in its entirety (it is too big).
- What is random sampling?
- Random sampling is where every member of the population has an equal chance of being chosen for your sample.
- Random sampling should ensure external validity (ie any results should generalise to the whole population).
- What is random allocation?
Random allocation is where every member of your sample has an equal chance of being allocated to your various “treatment” groups.
Random allocation helps ensure internal validity, ie the results enable us to assert that a causal relation between the independant variable IV and dependant variable DV exists in the event of a significant result.
- What are confounds?
Variables which are not relevant to the IV under study, but which introduce unwanted changes in the DV.
Random allocation can help remove this threat.
- Define the independant variable IV
The independent variable is the variable that is controlled and manipulated by the experimenter. For example, in an experiment on the impact of sleep deprivation on test performance, sleep deprivation would be the independent variable.
- What is the dependant variable DV?
The dependent variable DV is the variable that is measured by the experimenter.
For example, in an experiment on the impact of sleep deprivation on test performance, the scores on the test performance measure would be the dependent variable DV.
- What two measurements of mean are comonly used?
We consider both the population mean (usually written μ) and the sample mean (often written M).
19 Describe the mode.
The mode is the most frequent observation: “modish” is “fashionable”, ie what most people are doing.
- Define the median
The median is the middle number of a dataset arranged in increasing order. Both mode and median are generally uninfluenced by outliers.
- What is the most useful measure of dispersion?
Standard deviation SD is considered the most effective.
Written σ for the population, and s for the sample. s is a good estimator for σ, if you just have a sample.
- Define **varience **
- variance measures how far a set of numbers is spread out
- A variance of zero indicates that all the values are identical
- Variance is always non-negative
- Varience is the square of a standard deviation SD.
- Define nomal distribution.
The normal (or Gaussian) distribution is a function that represents the distribution of many random variables as a symmetrical bell-shaped graph.
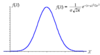
- Define percentile
“Percentiles” are used to describe, as a percentage, the area under the normal distribution to the left of a given point. The typical “given point” is described as a “z-score”, which is the distance of that point from the mean, the unit of distance being one standard deviation.
For each z-value, there corresponds a percentile between 0 and 100, and for each percentile, there is a z-value (which could be any number from large and negative to large and positive).