MMB-STATS-MARCH EXAM Flashcards
- Question 1:
Independent groups t-test:
What are the 6 assumptions that must be met?
1: You have one dependent variable that is measured at the continuous level.
#3: You should have independence of observations (no participant can be in both the control group and the intervention group)
- Question 1:
Independent groups t-test:
What tabs are needed to do the test?
(a)Given the result of Levene’s test, which row of the output will you interpret? Underline the correct one:
You access the test by going to Analyze >> Compare Means >> Independent samples t-test:
IV1 needs to be added with its 2 factors
- If Levine’s is sig < 0.5 then Second Row is read (Equal Variences not assumed)
- else if Levines sig > 0.5 the First Row is used (Equal Variences assumed)
-
Independent groups t-test:
(b) In the light of your decision in (a), report the result in the form t(?) = ?
SPSS also reports that t = 2.365 (the “t” column) and that there are 38 degrees of freedom (the “df” column).
t(df - degrees of freedom) = 2.365(value of t)
t(38) = 2.365
- Question 1 (c)
Independent groups t-test:
(c) state whether the result is significant at the level of p = .05
i. e LESS than .05 level (p < .05)
In this example, p = .023 (i.e. p < .05). Therefore, it can be concluded that males and females have statistically significantly different mean engagement scores. Or, phrased another way, the mean difference in engagement score between males and females is statistically significant. What this result means is that there is a 23 in 1,000 chance (2.3%) of getting a mean difference at least as large as the one obtained if the null hypothesis was true (the null hypothesis stating that there is no difference between the group means). Remember, the independent-samples t-test is testing whether the means are equal in the population.
5 Question 1
Independent groups t-test:
(d) Regardless of the answer to (c), specify which gender scored higher on the DV.
Data are mean ± standard deviation, unless otherwise stated. There were 20 male and 20 female participants. The advertisement was more engaging to male viewers (5.56 ± 0.29) than female viewers (5.30 ± 0.39). Hence males scored higher.
- Question 2
A researcher is interested in determining whether the ability to memorize nonsense syllables among the psychology faculty at her university differs from that for the general population. She uses a standard list of syllables for which the population average correct score is known to be …[x]….. In her faculty she obtains, from a sample of 12 lecturers, the following scores:
[data to be given in exam paper]
What is the appropriate statistical procedure to test her hypothesis?
The** one-sample t-test** is used only for tests of the sample mean (12 faculty members). Thus, the hypothesis tests whether the average of the sample (M) suggests that the 12 faculty members come from a population with a known mean (m) or whether it comes from a different population.
The “One Sample T-Test” is similar to the “Independent Samples T-Test” except it is used to compare one group’s average value to a single number
“The term “sample” refers to a portion of the population that is representative of the population from which it was selected.”
7 Question 2
Enter the data into SPSS. Which of the following results is the researcher likely to report? Underline as appropriate.
- Lecturers score significantly lower than the general population
- Lecturers score significantly higher than the general population
- There is no clear evidence of a difference between these lecturers and the general population.
The one-sample t-test assumes that the DV is normally distributed and there are no outliers.
Click Analyze > Compare Means > One-Sample T Test
Enter the population mean you are comparing the sample against in the Test Value:
8 Question 2:
One sample t test:
How do you read the results?
Moving from left-to-right, you are presented with the observed t-value (“t” column), the degrees of freedom (“df”), and the statistical significance (p-value) (“Sig. (2-tailed)”) of the one-sample t-test. In this example, p < .05 (it is p = .022). Therefore, it can be concluded that the population means are statistically significantly different. If p > .05, the difference between the sample-estimated population mean and the comparison population mean would not be statistically significantly different.
Look at the mean - and see if it is higher or lower to answer as well as the p
- **How do you check for outliers? **
- Click Analyze > Descriptive Statistics > Explore… on the main menu:
- Transfer the DV, into the Dependent List
- Click the plots button and you will be presented with the Explore: Plots dialogue box
- Keep the default Factor levels together in the -Boxplots- area, but deselect Stem-and-leaf in the -Descriptive- area and select Normality plots with tests
- Click the Continue button. You will be returned to the Explore dialogue box
- Click the Plots option in the -Display- area. This will result in only those options you selected in the Explore: Plots dialogue box being produced.
- Click OK!
10 How do you perform Shapiro-Wilk test for normality ?
The Shapiro-Wilk test is recommended if you have small sample sizes and are not confident visually interpreting Normal Q-Q Plots
significance value for this test is p = .847
If p < .05, the depression scores (dep_score) are not normally distributed. On the other hand, if p > .05, the scores are normally distributed.
Depression scores were normally distributed, as assessed by Shapiro-Wilk’s test (p > .05).
- Question 3:
A colleague points out that the lecturers should be compared, not with the general population, but with an age-matched subgroup of the population for which the average score is not x but y. Using the same data from the lecturers, but this different population average, which conclusion does this data support now?
Test for outliers and normaility before running the one-sample t-test again
Again the sample mean is not matched in number to the subgroup of the** population** (μ).
- Question 4: two-tailed test of significance
Novice and expert chess players were given 5 seconds to view a chessboard as it might appear 20 moves into the game. They were then asked to reproduce the placement of the pieces on the board. The total of the number of pieces accurately placed by the various participants were as follows:
A two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive.
DV should be measured at the interval or ratio level (i.e., they are continuous) YES score
IV should consist of two categorical, independent (unrelated) groups YES (novice and expert in 1 column!!!) labelled (0 and 1) or (1 and 2)
Normally we would - Test for outliers - then normaility - then homogeneity of variances using **Levine’s test **
13 Question 4: two-tailed test of significance
Which of the following statements do the data support? Underline as appropriate.
a. The experts perform this task better on average than the novices.
b. The novices perform better on average than the experts.
c. On the evidence available, the null hypothesis of no difference in performance between experts and novices cannot be rejected.
If you failed to meet the assumptions of the independent-samples t-test, you would consider running a non-parametric test.
In SPSS via analyze >> non-parametric tests: equivalents exist for the parametric t-tests and ANOVA (independent groups and repeated measures). BUT – there are only one-way options: there are no tests available on SPSS for doing two-way or multi-factorial ANOVAs.
When using a between-groups test such as one-way or multifactorial independent groups ANOVA, there is just one column for the DV, and you can rank cases using the Transform >> Rank Cases menu.
14. Question 5: Pearson’s chi-squared test
In dataset 2, IV1 represents the gender of a number of participants in a group difference study in which the clinical and control participants are encoded using IV2.
Your supervisor is concerned that the gender balance might be different between the clinical and control groups. Carry out a Pearson’s chi-squared test to determine whether this concern is justified. Report your result in the form χ2(?) = ?, p = ?
The chi-square test for independence, also called Pearson’s chi-square test or the chi-square test of association, is used to discover if there is a relationship between two categorical variables.
In order to run a chi-square test for association, you require the following:
» Two variables that are nominal/dichotomous (e.g., males/females).
» There are two or more groups in each variable.
15: Question 5: Pearson’s chi-squared test
List the 11 steps required to get the output (can do less but this gives more details)
- Click Analyze > Descriptive > Crosstabs…
- Transfer the (IV1) gender into the Row(s): box and the (IV2) variable (clinical and controls) into the Column(s): box by highlighting them and clicking on the relevant button. Also, select Display clustered bar charts.
- Click on the Statistics button. You will be presented with the Crosstabs: Statistics dialogue box
- Select Chi-square and then select Phi and Cramer’s V in the –Nominal– area
- Click the Contine button. You will be returned to the Crosstabs dialogue box
- Click the Cells button. You will be presented with the Crosstabs: Cell Display dialogue box
- Select Expected in the –Counts– area and Row, Column and Total from the –Percentages– area
- Click the Continue button. You will be returned to the Crosstabs dialogue box.
- Click the **Format **button. You will be presented with the Crosstabs: Table Format dialogue box
- Click the Continue button. You will be returned to the Crosstabs dialogue box
- Finally click OK!!!!!
16 Question5: Pearson’s chi-squared test
Report your result in the form χ2(?) = ?, p = ?
χ2(degrees of freedom /df ) = (valuea), p = (exact sig sone sided)
A chi-square test for association was conducted between gender and preference for performing competitive sport. All expected cell frequencies were greater than five. There was a statistically significant association between gender and preference for performing competitive sport,
χ2(1) = 5.195, p = .023.
- Question 5: Pearson’s chi-squared test
Regardless of whether the result is significant or not, how do the gender ratios differ in the two groups? Underline as appropriate:
- The clinical group has relatively more females than males compared to the control group
- The control group has relatively more females than males compared to the clincal group
We are not looking at absolute numbers but relative numbers. Eg looking for a gender imbalance.. Ratio! The Chi Squared tells us if the ratio is dignificantly different.
Different example look at chart.
By selecting to show a clustered bar chart in the Crosstabs procedure, you will have generated a good visual graph:
From these results, you can see that for “males”, the observed frequency was somewhat greater than expected for “yes” to competitive sports, and lower than expected for “no” to competitive sports, and in “females”, the other way around. This might lead you to suspect that there is an association between these two variables. You can test for this formerly in the next section.
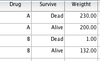
- Question 6: Pearson’s chi square test
You read in a published paper comparing two drugs, A and B, over a 24 month period, that out of [100] patients treated with the standard drug for the condition, drug A, [75] remained alive and [25] died, whereas out of [90] patients treated with the experimental drug B, [20] remained alive and [55] died.
Conduct a Pearson’s chi square test to find out which of the following conclusions is supported by this evidence:
- Drug A achieves a higher survival rate than drug B over 24 months
- Drug B achieves a higher survival rate than drug A over 24 months
- On this evidence, There is no significant difference on this evidence between the effects of drugs A and B.
Must Weight Cases to save time! Three colums (DRUG (0/1) SURVIVE (0/1) and their 4 weights.
The chi-square test for association tests for whether two categorical variables are associated (Drug A or B). Another way to phrase this is that this test determines whether two variables are statistically independent.
» Two variables that are nominal/dichotomous (e.g., males/females in this case Drug A and Drug B).
» There are two or more groups in each variable. (Alive or Dead in this case)
19: Question 7: paired-samples t-test
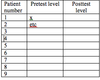
A pre-test/post-test study on the effectiveness of a drug intended to reduce anxiety on a small sample of patients gave the following data, where the DV represents the anxiety level:
What assumptions are required?
Assumption #1: You have one dependent variable that is measured at the continuous (i.e., ratio or interval) level.
Assumption #2: You have one independent variable that consists of two categorical, related groups or matched pairs (i.e., adichotomous variable). “Related groups” indicates that the two groups are not independent. The primary reason for having related groups is having the same participants in each group. It is possible to have the same participants in each group when each participant has been measured on two occasions on the same DV
Assumptions #3 there should be no significant outliers in the differences between the two related groups;
Assumptions #4: the distribution of the differences of the DV between the two related groups should be approximately normally distributed.
- Question 7: paired-samples t-test
**What are the Null and Alternative Hypothesis? **
The null hypothesis (H0) for a paired-samples t-test is:
H0: the population mean difference between the paired values is equal to zero (i.e., µdiff = 0).
And the alternative hypothesis (HA) is:
HA: the population mean difference between the paired values is not equal to zero (i.e., µdiff ≠ 0).
21: Question 7 paired samples t test
How do you calculate a difference score in SPSS? And following this what two assumptions must be met?
- Click Transform > Compute Variable… on the main menu
- Type “difference” (without the quotation marks) into the Target Variable: box. This will mean that the newly-created variable is called difference. Then, to calculate the difference between related groups (i.e., paired values), in the Numeric Expression: box, type in “pretest - posttest” (without the quotation marks)
- Click the OK button. You will be returned to the Data View window where you will see that your new variable
- Assumption #3 There should be no significant outliers in the differences between the two related groups (difference score)
- Assumptions #4: the distribution of the differences of the DV between the two related groups should be approximately normally distributed. (use the difference score)
- Question 7:
How do you perform the Paired Samples T test?
- Click Analyze > Compare Means > Paired-Samples T Tst
- Transfer the variables pre and post into the Paired Variables: box
- (probably swap the variables round to post - pre)
- Click the Option button. You will be presented with the Paired-Samples T Test: Options dialogue box
- Click the Continue button and you will be returned to the Paired-Samples T Test dialogue box
- Finally click OK to get output
- Question 7:
How do you interpret result of a paired sampled T test?
write the conclusion in the form t(?) = ?
t(degrees of freedom df) = 6.352, p < .0005
t(19) = 6.352, p < .0005.
Moving from left-to-right columns, you are presented with the obtained t-value (the “t” column), the degrees of freedom (the “df” column), and the statistical significance value (i.e., p-value) (the “Sig. (2-tailed)” column) of the paired-samples t-test. If p < .05, this means that the mean difference between the two related groups is statistically significant. Alternatively, if p > .05, you do not have a statistically significant mean difference between the two related groups. In this example, the statistical significance level is stated as .000, which means p < .0005 (i.e., this satisfies p < .05).
24. Question 8: one-way ANOVA
In dataset 3, carry out a one-way ANOVA using IV1 (clinical group) as the factor and DV1 as the DV. You have no a priori hypothesis as to likely effects, but are interested in any significant pairwise differences between group means.
What are the key Assumptions needed to run?
Assumption #1: You have one dependent variable that is measured at the continuous level.
Assumption #2: You have one independent variable that consists of two or more categorical, independent groups.
Assumption #3: You should have independence of observations, which means that there is no relationship between the observations in each group of the independent variable or between the groups themselves.
Assumptions #4, #5 and #6 No outliers, must have normality and homogeneity of variances (i.e., the variance of the dependent variable is equal in each group of the independent variable)
- Question 8: one-way ANOVA
What is the procedure to carry out the one-way Anova test using IV1 (clinical group) as the factor and DV1 as the dependent variable
- Click Analyze > Compare Means > One-Way ANOVA…
- Transfer the DV(DV1) into the Dependent List: box and the IV, IV1(clinical group), into the Factor: box,
- Click the button and you will be presented with the One-Way ANOVA: Options dialogue box,
- Select the Descriptive, Homogeneity of variance test and **Welch **checkboxes in the –Statistics– area and select the Means plot checkbox.
- Click the **Continue ** button and you will be returned to the One-Way ANOVA dialogue box
- Click the PostHoc button and you will be presented with the One-Way ANOVA:
- Select the Tukey checkbox in the –Equal Variances Assumed– area and the Games-Howell checkbox in the –Equal Variances Not Assumed– area
- Click the Continue button and you will be returned to the One-Way ANOVA dialogue box.
- Finally Click OK!
26. Question 8: one-way ANOVA
How do you test for homogeneity of variences? ]
The assumption of homogeneity of variances states that the population variance for each group of your independent variable is the same. If the sample size in each group is similar, violation of this assumption is not often too serious. However, if sample sizes are quite different, the one-way ANOVA is sensitive to the violation of this assumption.
The assumption of homogeneity of variances is tested using Levene’s test of equality of variances, which is but one way of determining whether the variances between groups for the dependent variable are equal. p must be > 0.05. The result of this test is found in the Test of Homogeneity of Variances table, as highlighted below:
There was homogeneity of variances, as assessed by Levene’s test for equality of variances (p = .120).
27. Question 8: one-way ANOVA
How do you report findings when results when homogeneity of variances is met?
(a) report the result of the omnibus F test of the data in the form F(?, ?) = ? p = ?
F(?, ?) = ? p = ?
F(df betwengroups, df within groups) = F p = Sig.
F(3, 27) = 8.316, p < .0005.
You can interpret the standard one-way ANOVA and, if this test is statistically significant, either: (a) interpret the results from the Tukey post hoc test to understand where any difference(s) lie; or (b) run contrasts to investigate specific differences between groups. The one-way ANOVA result is found in the ANOVA table, as shown below:
28. Question 8: one-way ANOVA
How do you report findings when homogeneity of variances is NOT met?
(a) report the result of the omnibus F test of the data in the form F(?, ?) = ? p = ?
This means that you cannot interpret the standard one-way ANOVA, but must use a modified version of the ANOVA. In this example, the Welch ANOVA is used.
The result of the Welch’s ANOVA is found in the Robust Tests of Equality of Means table
Welch’s F(3, 14.574) = 14.821, p < .0005.
31: Question 8 - one way anova
Pairwise Comparisons
(c) Which of the following was true (underline):
- The autism group scored significantly higher than the Williams syndrome group
- The Williams syndrome group scored significantly higher than the autism group
- There was no significant difference in scores between the autism and Williams groups.
Need to do a post hoc test.
This comparison states that the mean CWWS score in the “Low” group is 1.72762 higher than the “Sedentary” group. To determine whether this mean difference is statistically significant, you need to consult the “Sig.” column, which presents the p-value. For this comparison, the p-value is .092 (i.e., p = .092) therefore, the mean difference between these two groups is not statistically significant.
- Question 8:
(d) The Williams syndrome group average was significantly different from one of the control groups. Which one?
- IQ matched controls
- Age matched controls.
We don’t know but it is likely to be age matched controls?
Image of column meanings for a Tukey post hoc test
36: Question 9: 2-way Anova
What is the procedure to check for normality when setting up a 2-way Anova in SPSS?
use the Shapiro-Wilk test
If the assumption of normality has been violated, the “Sig.” value will be less than .05 (i.e., the test is significant at the p < .05 level). If the assumption of normality has not been violated, the “Sig.” value will be greater than .05 (i.e., p > .05). This is because the Shapiro-Wilk test is testing the null hypothesis that your data’s distribution is equal to a normal distribution.
39. Question 9 2-way Anova
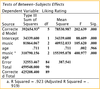
(a) report the omnibus F test for the whole dataset, and whether or not it is significant at the p = .05 level:
Need to look at the corrected model in the tests of between subjects effects.
F(?,?)=?
F(df in corrected model column), (df Error) = F in corrected model colum
Hence, F(5,84) = 202.639
p < 0.05 therfore it is significant at the .05 level. YES
- Question 9 2-way Anova
(b) State whether or not the following are significant:
Use plots to decipher the data! Make sure to add IVs in the plots area when running the 2 way Anova!
- main effect of gender: Yes/no………………………………..
- main effect of age: Yes/no……………………………………..
- age by gender interaction: Yes/no ………………………….
If there is a significant interaction is it a real interaction? Quantatitive: Different slopes and crossing lines signify a strong interaction not near parallel
Qualitatitive: Same slope, near parrallel may be a sign of celing, floor or scale effects.
- This plot shows a main effect of leg length
- No main effect of gender
- There is likely no significant interaction as the lines are very near parallel.
41. Question 9 2-way Anova
(c) by examining a line plot or otherwise, underline the correct alternative among the following options:
- There is no clear age*gender interaction
- There is a quantitative age*gender interaction
- There is a qualitative age*gender interaction
How do we know?
Quantatitive: Different slopes and crossing lines signify a strong interaction not near parallel
Qualitatitive: Same slope, near parrallel may be a sign of celing, floor or scale effects.
This plot:
Leglength is a main effect
Sex not effect
There is an interaction as it is non parallel and is crossing.
- Question 10 repeated measures ANOVA
How do we read the pairwise comparisons from the Bonferroni Correction
Remember we are looking for a lower score for the mean!!!
- Tests For Normality - Kolmogorov-Smirnov Test
- Dataset 7 contains data reporting the average response times (variable “RT”) for three groups of individuals, coded using the variable “grp”. These groups comprise an autism group, Williams syndrome group and an age-matched control group.
Parametric tests comparing these groups on the DV assume that it is normally distributed within each group. Carry out a test for normality for this DV using the Kolmogorov-Smirnov test. What p-values do you find for the three groups?
p = ……………, …………., …………………..
- Click Analyze > Descriptive Statistics > Explore…
- Group must go in the factor list (containing the three levels of groups and put the DV in teh dependant list
- Click in PLOTS and deselect Stem-and-leaf in the –Descriptive– area and select Normality plots with tests,
- Click Continue and OK
If the Kolmogorov-Smirnov test ig p > 0.5 it assumes normality. Usally as .200*
Answer will be Gp1 p =200* Gp2 p = 200* and Gp 3 p = 200*
52: Question 13.
13. The same three groups have also been measured on their ability to detect absolute pitch in speech, their percentage scores being recorded as the variable “APS”. Carry out a test for outliers within these groups using the Explore menu and determining their presence via box plots.
(a) How many outliers, if any, do you find?
……………………
Any data points that are more than 1.5 box-lengths from the edge of their (brown-yellow) box are classified by SPSS Statistics as outliers and are illustrated as circular dots. Any data points that are more than 3 box-lengths away from the edge of their box are classified as extreme points (i.e., extreme outliers) and are illustrated with an asterisk (*).
55. Question 14 Regression Model with 2 IVs
b. What is the value adjusted R2 for this model?
Look under model summary the R2 will be there.
56 Question 14 Regression Model
c. In the forced entry (entered into the equation in one step) regression, are the individual IVs significant?
- Extra Yes….no….
- Imp Yes….no….
You can test for the statistical significance of each of the independent variables.
If p < .05, you can conclude that the coefficients are statistically significantly different to 0. Thet-value and corresponding p-value are located in the “t” and “Sig.” columns, respectively, as highlighted below:
58. Question 14 Regression Model Multicolliniarity
e. Diagnose the discrepancy between the results of your analysis at c. and d. above, and provide evidence for it, in the following form of words:
The value of ………………….is (less than/more than*) ………………………, indicating the presence of ……………..
* delete as applicable.
Need to tick statisitcs and Colliniarity Diagnostics and run the regression again to find this out
The value of Tolerance is less than 0.25, indicating the presence of multicolliniarity.
61 Question 15 Factor Analysis
Perform an exploratory factor analysis on this data, using a scree plot to determine the number of factors (there are between one and four factors).
(a) What is the value of the KMO measure of sampling adequacy? ……………………….
Under the KMO test there is a number giving it’s value.
62. Question 15 Factor Analysis
(b) How many factors should be extracted? ………………………..
Decide number of factors from number of dots above the elbow. of the scree plot - likely to be 3 or 4
This example has 3 -
63 Question 15 Factor Analysis
(c) Carry out a PRINCIPAL AXIS FACTORING and use a PROMAX (oblique) rotation. Examine the Factor Correlation Matrix (this should be at or near the bottom of the output screen). What is the value of the largest off-diagonal covariation that you observe?
In this example looking down there is the number 1.00 on the diagonal.
64 Question 15 Factor Analysis
(d) This number is sufficiently small to justify the assumption that the factors are orthogonal. So now carry out a principal axis factoring with VARIMAX rotation of factors. Under “options”, use the value of .4 as the cutoff to suppress small coefficients and sort them by size. Examine the rotated factor matrix and describe the composition of the factors below (n.b. you may not need to complete all four entries if you have found fewer than four factors).
For example, if q1, q2 and q3 were to load positively on factor 1, and if q4 were to load negatively on it, you would write Factor 1: q1, q2, q3, – q4.
Factor 1:
Factor 2:
Factor 3:
Factor 4:
Look at the numbers - are they positive or negative? In this example the negative numbers are the odd ones out in the Factor lists..
Factor 1: + Q5(Funny), + Q7(Entertaining), - Q2(creepy)
