Level 1C Flashcards
Evaluate 132.
169
Evaluate 162
256
Evaluate 192
361
Evaluate 212.
441
Evaluate 242
576.
Evaluate 272
729.
Evaluate 302
900
Evaluate 43
64
Evaluate 63
216
Evaluate 83
512
Evaluate 103
1000
Evaluate 123
1728
Evaluate 143
2744
Evaluate 25
32
Evaluate 28
256
Evaluate 211
2048
Evaluate 214
16384
What are the five platonic solids?
Tetrahedron, Hexahedron (Cube), Octahedron, Dodecahedron, Icosahedron.
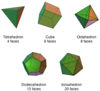
Describe the characteristics of a tetrahedron.
A tetrahedron has the following properties:
1) 4 equilateral triangle faces
2) 4 vertices
3) 6 edges
Describe the characteristics of a hexahedron (cube).
A hexahedron has the following characteristics:
1) 6 square faces
2) 8 vertices
3) 12 edges
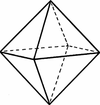
Describe the characteristics of an octahedron.
An octahedron has the following characteristics:
1) 8 equilateral triangle faces.
2) 12 edges
3) 6 vertices
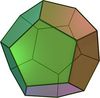
Describe the characteristics of a dodecahedron.
A dodecahedron has the following characteristics:
1) 12 regular pentagon faces
2) 30 edges
3) 20 vertices
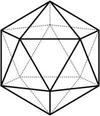
Describe the characteristics of an icosahedron.
An icosahedron has the following characteristics.
1) 20 equilateral faces
2) 30 edges
3) 12 vertices
What are the prime numbers from 100 to 120?
101, 103, 107, 109, 113
What are the prime numbers from 120 - 140?
127, 131, 137, 139
Find a pythagorean triple whose smallest side is 11.
11, 60, 61
Find a pythagorean triple whose smallest side is 12 and is not a multiple of another pythagorean triple
12, 35, 37
Find a pythagorean triple whose two smallest sides are 20 and 21.
20, 21, 29
*This is a commonly used pythagorean triple since the numbers have a different relationship than the smaller ones.
What is the sum of the numbers in the nth row of the pascal’s triangle?
2n
*Remember the top row is the 0th row.
1 = 20
1 + 1 = 21
1 + 2 + 1 = 22
1 + 3 + 3 + 1 = 23
1 + 4 + 6 + 4 + 1 = 24
How many even factors does 120 have?
12.
*First find the number of factors using the # of factors formula. In this case the prime factorization is (2^3)*3*5=120 so the # of factors is (3+1)(1+1)(1+1) = 16.
**Then find the # of odd factors by multiplying the exponents of the odd prime factors so (1+1)(1+1)=4 So the # of even factors is 16-4.
***Watch this video to learn more about it
How many odd factors does 180 have?
6.
*Find the prime factorization of 180. So 180 = (2^2)(3^2)*5
**The odd factors are found by looking at the odd prime factors. So (2+1)(1+1) = 6.
What is the product of the factors of 48?
485
*First find the # of factors so 48 = 24*3 so the number of factors is (4+1)(1+1) = 10.
**Since the 10 factors are factor pairs as shown: 1*48, 2*24, 3*16, 4*12, 6*8 they all have a product of 48. When all the 10 factors are multiplied together you get 485.
***Watch this video to learn more.
Evaluate 1052
11025.
*This is found by multiplying 10*11 = 110 and then adding 25 to the end. So 11025.
Evaluate 1152
13225.
Multiply 11*12 = 132 and then add 25 to the end. 13225.
Evaluate 1252
15625.
*Multiply 12*13 = 156. Then add 25 to the end to get 15625.
Write 0.2444444(repeating) as a fraction.
11/45
*First multiply by 10 so that it becomes 2.444444 (repeating).
**Then convert to a fraction so 2 4/9
***Then multiply by 1/10 to undo the original multiplication 22/9 * 1/10 = 22/90 = 11/45
Write 0.241515151515 (repeating) as a fraction.
797/3300
*First multiply by 100 so only the repeating part is on the other side of the decimal. 0.2415151515*100 = 24.15151515…
*Then convert to a fraction 24 15/99 = 24 5/33 = 797/33.
*Then multiply by 1/100 to undo multiplying by 100. Thus (797/33)*(1/100) =797/3300.
Given the number and type of faces of a polyhedron, how do you find the number of edges?
Each edge of a polyhedron is made up of an edge from 2 of the faces. Thus the total number of edges on all the polygon faces is divided by 2 to find the number of edges in the polyhedron.
What is the decimal equivalent to 1/40?
0.025
*When dealing with 40th’s the key is to go .025 above or below a know amount. For example, 3/40 is .025 more than 2/40 = 1/20 = .05 so 3/40 is .075.
What is the decimal equivalent of 9/40?
.225
*When dealing with 40th’s the key is to go .025 above or below a know amount. For example, 9/40 is .025 less than 10/40 = 1/4 = .25 so 9/40 is .225.
What is the decimal equivalent of 17/40?
.425
*When dealing with 40th’s the key is to go .025 above or below a know amount. For example, 17/40 is .025 more than 16/40 = 4/10 = .4 so 17/40 is .425.
What is the decimal equivalent to 31/40?
.775
*When dealing with 40th’s the key is to go .025 above or below a know amount. For example, 31/40 is .025 more than 30/40 = 3/4 = .75 so 31/40 is .775.
What is the decimal equivalent of 1/80?
.0125
The key to 80th’s is to add or subtract .0125 from a 40th. For example, 5/80 is .0125 is
7/80
.0875
7/80 is .0125 less than 8/80 = .1
What is the decimal equivalent to 17/80?
.2125
17/80 is .0125 more than 16/80 = 2/10 =.2
What is the decimal equivalent of 41/80?
.5125
41/80 is .0125 more than 40/80 = .5.
What is the decimal equivalent to 71/80?
.8875
71/80 is .0125 more than 70/80 = 7/8 =.875
For two numbers A and B, what is the product of their GCD and LCM?
A*B
*The product of the GCD and LCM of two number is always equal to the product of the two numbers.
What is the product of the GCD and the LCM of 24 and 32?
768.
The GCD of the two numbers is 8 and the LCM is 96. 96*8=768. However, it is easier to just multiply the two numbers together. 24*32 = 768.
