Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

Level 1 MATHCOUNTS > Level 1B > Flashcards

Level 1B Flashcards

1
Q

33

A

27

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

What is the decimal equivalent of 1/12?

A

0.0833333 (the 3 repeats)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

What are the prime numbers that are greater than 60 but less than 80?

A

61, 67, 71, 73, 79

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

What is the decimal equivalent to 6/11?

A

0.54545454…

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Evalutate 210

A

1024

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

What is decimal equivalent to 11/12?

A
  1. 9166666

I remember the twelths by recognizing that 12*(8 1/3) = 100. Thus I subtract 8 1/3 from 100 to get 91 2/3.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Evaluate 20C18

A

Evaluating 20C18 would be a lot of writing. Instead we realize that choosing 18 things from a group of 20, leaves 2 things behind. Thus 20C18 = 20C2 = (20*19)/(2*1) = 190.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

How is the GCF of a set of numbers calculated using the prime factorization of the numbers?

A

The GCF of a set of numbers is calculated by multiplying together all of the prime numbers that are in all of the numbers. If, for example, they all contain a 22 then two twos are multiplied as part of the GCF. Check out this video to see some examples of this.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Evaluate 213

A

8192

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

What is the decimal equivalent of 2/7

A

0.285714285714…

Note that the sevenths cycle through the sam 6 numbers and just start at a different place and those are the multiples of 14 or 1 more than a multiple of 14 (57, 71, 85)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

152

A

225

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

What are the prime numbers that are greater than 80 but less than 100?

A

83, 89, 97

*many student include 91 as a prime number when it is actually the product of 7 and 13.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

What is the divisibility rule for 18?

A

A number is divisible by 18 if it is divisible by 2 and by 9.

*Note: if a number can be written as the product of two relatively prime numbers then it takes on both of the divisibility rules.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

53

A

125

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

What are supplementary angles?

A

Two angles whose measure have a sum of 180 degrees. If angle A and angle B are supplementary, then we say that angle A is the supplement of angle B (and vice versa).

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

What is the decimal equivalent to 1/7?

A

0.142857142857…not the repeating part.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Name all pythagorean triples whose smallest side is less than 10.

A

(3, 4, 5), (6, 8, 10), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41)

*A pythagorean triple is a set of three integers that satisfy the pythagorean theorem.

**Note that (6, 8, 10) is just a multiple of (3, 4, 5). Multiples of pythagorean triples are also pythagorean triples.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Evaluate 27

A

128

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

The numbers 1 - 400 are written on slips of papers. How many of the papers will include the digit 5?

A

76.

*from 1 - 100 every digit (other than 0) appears 20 times but in 19 numbers. So for each hundred a 5 will appear in the ones/tens place in 19 numbers (20 times - twice for 55). So 19*4 = 76.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

Evaluate 5!

A

5! = 5*4*3*2*1 = 120

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Evaluate 7!

A

7! = 7*6*5*4*3*2*1 = 5040

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

Evaluate 952.

A

9025.

The algorithm we use is to take the tens digit and multiple it by the next integer. So 9*10 = 90 and then we append 25 to get 9025.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

What is the first number greater than 2000 that is divisible by 15?

A

The divisibility rule for 15 is it must be divisible by 3 and 5. Thus we start looking at multiples of 5. 2005 is not divisible by 3, but 2010 is, thus the answer is 2010.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

What is the decimal equivalent to 2/11?

A

0.18181818…

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

What is the decimal equivalent of 5/7?

A

0.714285714285…

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

How do you find the LCM of a set of numbers using the prime factorization of the numbers?

A

For each prime number in one of the prime factorizations you take the highest power of that prime number that is the prime factorizations. If you multiply each of these together you get the Least Common Multiple. Check out this video to see an example of this.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q

Evaluate 752.

A

5625.

The algorithm we use is to take the tens digit and multiple it by the next integer. So 7*8 = 56 and then we append 25 to get 5625.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
29
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
30
Q

What is the decimal eqivalent to 3/7?

A

0.428571428571…

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
31
Q

Evaluate 552.

A

3025.

The algorithm we use is to take the tens digit and multiple it by the next integer. So 5*6 = 30 and then we append 25 to get 3025.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
32
Q

What is the decimal equivalent to 1/9?

A

0.1111111 (repeating)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
33
Q

What is the combination formula? i.e. how many ways can you pick r things from a group of n things?

A

nCr = n(n-1)…(n-r+1)/r!

For example, 7C3 = (7*6*5)/(3*2*1)

and 12C5 = (12*11*10*9*8)/(5*4*3*2*1)

*Remember combinations are used when the order that you choose things doesn’t matter.

*Watch this video if you want to learn more about why combinations work.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
34
Q

Let ABC be a three-digit integer. What is the value of ABC*1001?4

A

ABC,ABC.

**This is significant because 1001 factors nicely to 7*11*13. So a number like 144,144 can be factored quickly because 144,144 = 144*1001 = 24*32 *7*9*11.

**This same fact is true about other similar numbers such as 10001*ABCD = ABCDABCD.

35
Q

242

A

576

36
Q

What is the decimal equivalent to 7/11?

A

0.63636363…

37
Q

The natural numbers from 1 - 100 are written on a piece of paper. How many times is the digit 3 written?

A

20

*It occurs 10 times in the ones place (3, 13, …, 93) and 10 times in the tens place (30, 31, …39). Note that it occurs twice when 33 is written.

**This is true for all digits except for 0 since we don’t write 0 in a 10’s place. However, it IS true for 0, if you are looking from 201 - 300 (for example).

38
Q

302

A

900

39
Q

What is the decimal equivalent to 4/9?

A

0.4444444 (repeating)

40
Q

What is the decimal equivalent to 9/11?

A

0.818181818181…

41
Q

What is the decimal equivalent to 4/11?

A

0.36363636…

42
Q

Is 4058 divisible by 18?

A

No. 4058 is divisble by 2 since it is even, but it is not divisible by 9 because the sum of the digits is 17.

43
Q

Can you draw the pascals triangle through row 8 pretty much from memory? (Row 0 is the first 1)

A
44
Q

How many prime numbers are there from 1 - 100?

A

25

(can you name them quickly?)

2, 3, 5, 7, 11

13, 17, 19, 23, 29

31, 37, 41, 43, 47

53, 59, 61, 67, 71

73, 79, 83, 89. 97

45
Q

The permutation formula is aPb. Where you have “a” and “b” of them are permuted (arranged). What is the formula to calculate how many arrangements are possible? Essentially, what does aPb equal?

A

aPb = a * (a-1)*(a-2)*…*(a-b+1)

46
Q

Is 84,456 divisible by 36.

A

Yes! Since the sum of the digits is 8+4+4+5+6 = 27 it is divisible by 9 and the last two digits form 56 which is divisible by 4, so the number is divisible by 36.

47
Q

Evaluate 3!

A

3! = 3*2*1 = 6

48
Q

What is the prime factorization of 1001?

A

1001 = 7*11*13

This is significant because 7, 11, and 13 are all difficult to check for divisibility.

49
Q

List all the triangular numbers less than 100.

A

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91

*The triangular numbers are each the sum of the first “n” numbers. So 36 is the 8th triangular number because 1+2+3+4+5+6+7+8=36.

**So you can use the formula n*(n+1)/2

50
Q

What i the divisibility rule for 15?

A

A number is divisible by 15 if it is divisible by 3 and by 5.

51
Q

What is the decimal equivalent to 10/11?

A

0.90909090…

52
Q

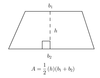
What is the formual for the area of a trapezoid?

A

The formula is given below - do you know why it works?

53
Q

What is the formula for the number of ways to arrange the letters in the word MISSISSIPPI?

A

The letter arrangement formula takes the number of letters factorial divided by the number of repeated letter factorial. Thus the denominator is what it is because there are 4 S’s, 4 I’s, and 2 P’s. Make sure you know why this works. Check out this video. Also, check out these examples: Example 1 and Example 2.

54
Q

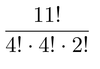
What is the divisibility rule for 36?

A

A number is divisible by 36 if it is divisible by 4 and by 9.

*Note - the divisibility rule is not 3 and 12 or 2 and 18 because those numbers are not relatively prime to each other (even thought 2 and 3 are primes).

55
Q

182

A

324

56
Q

What is the decimal equivalent to 3/11?

A

0.27272727…

57
Q

What are complementary angles?

A

Two angles, the sum of whose measure is 90 degrees. If angle A and angle B are complementary to each other then A is said to be the complement of B (and vice versa).

58
Q

Evaluate 19*31

A

.589.

**A fast and efficient way to multiply is to use difference of square multiplication. 19*31 = (25 - 6)(25 +6) = 252 - 62 = 625 - 36 = 589.

59
Q

The natural numbers 301 - 400 are written on a piece of paper. How many times is the digit 7 written?

A

20.

*It occurs 10 times in the ones place (307, 317, …, 397) and 10 times in the tens place (370, 371, …379). Note that it occurs twice when 377 is written.

**This is true for all digits (except 3 - which would have an additional 100 times from the hundreds digit.

60
Q

Evaluate 24

A

16

61
Q

What is the smallest 5 digit number that is divisible by both 15 and 18?

A
  1. We create the number by realizing it must be divisible by 3 and 5 and it must be divisible by 2 and 9. Thus 2 and 5 means divisible by 10, so it will end in 0. Thus we need the sum of the digits to be 9 and the first number that has a 0 at the end which accomplished this is 10080.
62
Q

What is the decimal equivalent to 5/11?

A

0.45454545…

63
Q

73

A

343

64
Q

What is the formula for the area of a triangle?

A

Note the two different cases. 1) The height is inside the triangle 2) The height is outside the triangle

65
Q

93

A

729

66
Q

133

A

2197

67
Q

What is the decimal equivalent of 4/7?

A

0.571428571428…(repeating the 6 digits).

68
Q

What is the decimal equivalent of 5/12?

A

0.4166666 (6 repeating)

I remember the twelths by recognizing that 12*(8 1/3) = 100. Thus I multiply by the numerator by 8 1/3. So 5*8 1/3 = 41 2/3. So 5/12 would be (41 2/3)/100

69
Q

How many natural numbers from 1 - 100 include a 6 as one of its digits?

A
  1. There are 20 instances of 6 from 1 - 100, however one of them, 66, has 6 occurring twice. Thus, there are 19 numbers.
70
Q

What is the procedure for finding the number of positive integer factors of a positive integer?

A

1) Find the prime factorization of the number.
2) Add 1 to each of the exponents.
3) Multiply those sums together.
4) Example: 144 = 24*32 thus the number of factors is (4+1)(2+1) = 15.

Watch this video and this video to learn more.

71
Q

212

A
72
Q

272

A

729

73
Q

Evaluate 28*52.

A

1456.

**A fast and efficient way to multiply is to use difference of square multiplication. 28*52 = (40 - 12)(40 + 12) = 402 - 122 = 1600 - 144 = 1456.

74
Q

What is the formula of the sum of the angles in a polygon with n sides?

A

180(n - 2). So for example, the sum of the angles in a decagon is 180(10-2) = 1440.

75
Q

What is the decimal equivalent to 1/11?

A

0.0909090909…

76
Q

What is the decimal equivalent of 6/7?

A

0.857142857142…

77
Q

113

A

1331

I remember this one as the 3rd row of the pascal’s triangle. Did you know that the rows of the pascal’s triangle form the powers of 11?

78
Q

Evaluate 99*101.

A

9,999.

**A fast and efficient way to multiply is to use difference of square multiplication. 99*101 = (100 - 1)(100 + 1) = 1002 - 12 = 10000 - 1 = 9999.

79
Q

3375

A
80
Q

What is the decimal equivalent to 8/11?

A

0.72727272…

81
Q

Evaluate 18*22.

A

396.

**A fast and efficient way to multiply is to use difference of square multiplication. 18*22= (20 - 2)(20 + 2) = 202 - 22 = 400 - 4 = 396.

82
Q

What is the decimal equivalent for 7/12?

A

0.5833333 (3 repeating).

I remember the twelths by recognizing that 12*(8 1/3) = 100. Thus I multiply by the numerator by 8 1/3. So 7*(8 1/3) = 58 1/3. So 5/12 would be (58 1/3)/100

83
Q

What is the decimal equivalent to 7/9?

A

0.777777 (repeating)

84
Q

122

A

144

Level 1 MATHCOUNTS (3 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions