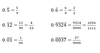Level 1A Flashcards
To master basic facts that are essential to high performance in MATHCOUNTS.
What is the divisibility rule for 3?
If the sum of the digits of the number are divisible by 3, then the number is divisible by 3.
What is the sum of the first n odd natural numbers?
The sum of the first n odd natural numbers is n^2. This is easy to see and leads to some cool insights: 1 = 1 + 3 = 4 (2^2) 1 + 3 + 5 = 9 (3^2) 1 + 3 + 5 +7 = 16 (4^2) This pattern explains why the difference between n^2 and (n+1)^2 is (2n+1). Note: the formula 2n - 1 can tell you which odd number you are on. For example, 9 is the 5th odd number because when you solve the problem 2n - 1 = 9 you get n = 5.
Evaluate 262
676
What is the decimal equivalent of 11/16?
0.6875
What is the divisibility rule for 8?
If the last three digits is a three-digit number that is divisible by 8, then the number is divisible by 8.
Evaluate 29
512
What is the decimal equivalent of 5/6?
0.83333333 (The 3 is repeating)
Evaluate 142
196
What is the divisibility rule for 2?
The number is an even number.
Evaluate 232
529
What is the divisibility rule for 4?
If the tens digit and ones digit form a two-digit number that is divisible by 4, then the number is divisible by 4.
What is the decimal equivalent of 5/16?
0.3125
What is the divisibility rule for 10?
If the last digit is a 0, then the number is divisible by 10.
What is the divisibility rule for 5?
If the final digit is 0 or 5, then the number is divisible by 5.
What is the divisibility rule for 9?
If the sum of the digits of a number is divisible by 9, then the number is divisible by 9.
Evaluate 23
8
Evaluate 172
289
What is the decimal equivalent of 3/8?
0.375
What is the decimal equivalent of 7/16?
0.4375
Lis all the prime numbers greater than 40 but less than 60.
41, 43, 47, 53, 59
Evaluate 212
4096
List all the prime numbers less than 20.
2, 3, 5, 7, 11, 13, 17, 19
Evaluate 452
2025 The key is to multiple the tens digit times one more than the tens digit and then appened a 25. So 4*5 = 12 then append 25 and you get 2025. The reason for this is because of the differnece of squares. (45+5)(45-5) = (50)(40) but also 45^2 -25. Thus (50)(40) is 25 less than 45^2.
What is the divisibility rule for 7?
This requires an algorithm to follow. Here are the steps: 1) Remove the ones digit - which effectively shortens the number by 1 digit. 2) Multiply the number removed by 2. 3) Subtract that from the new number. 4) If the result is divisible by 7, then the number is divisible by 7. 5) If you are not sure, then repeat steps 1 - 4 until you get a number you know is divisible by 4. Example 1 - 224 Remove 4 and multiply it by 2 to get 8. Subtract this from 22 to get 14. Since 14 is divisible by 7, then 224 is divisible by 7. Example 2 - 1288 Remove the 8 and multiply it by 2 and then subtract from 128 - 16 = 112. If you aren’t sure about 112 then remove 2 and multiply by 2 and then subtact 4 from 11 to get 7. Since 7 is divisible by 7, then 1288 is divisible by 7.
Evaluate 26
64
What is the decimal equivalent of 15/16?
0.9375
List all the numbers less than or equal to 100 that have an odd number of factors.
1, 4, 9, 16, 25, 36, 49, 64, 81, 100. **Perfect squares have an odd number of factors because you can list all factors as factor pairs, except for the square root which only counts once.
What is the decimal equivalent of 5/8?
0.625
What is the decimal equivalent of 1/8?
0.125
What is the decimal equivalent of 1/6?
0.16666666 (The 6 is repeating)
What is the divisibility rule for 6?
If the number is divisible by 2 and 3, then the number is divisible by 6.
What is the decimal equivalent of 13/16?
0.8125
What is the divisibility rule for 11?
This requires an algorithm to follow: 1) Start with the first digit and add every other digit to get a sum. 2) Add together the other digits. 3) Subtract the two sums. If the difference is a multiple 11 (including 0), then the number is divisible by 0. Example 1 - Is 132,649 divisibly be 11. Starting with the first digit 1 + 2 + 4 = 7 The other digits sum is 3 + 6 + 9 = 18. 18 - 7 = 11 thus 132,649 is divisibly by 11.
What is the divisibility rule for 12?
If the number is divisible by 3 and by 4, then the number is divisible by 12.
List all the prime numbers greater than 20 but less than 40.
23, 29, 31, 37
Evaluate 202
400
Evaluate 29^2
841
What is the decimal equivalent of 9/16?
0.5625
What is the decimal equivalent of 1/16?
0.0625
List the fibonacci sequence for numbers less than 150?
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 - you should only select a 5 if you can list these out without having to do the sums.
What is the decimal equivalent of 3/16?
.1875
What is the decimal equivalent of 7/8?
0.875
Evaluate 322
1024
Evaluate 112.
121
Evaluate 352
1225 The key is to multiple the tens digit times one more than the tens digit and then appened a 25. So 3*4 = 12 then append 25 and you get 1225. The reason for this is because of the differnece of squares. (35+5)(35-5) = (40)(30) but also 35^2 -25. Thus (40)(30) is 25 less than 35^2.
What is the sum of the first “n” positive integers? (i.e. what is the sum of 1 + 2 + 3 + 4 + …+ n)
The sum of the first “n” positive integers is n(n+1)/2.
What are the three versions of the formula that connects distance (d), rate (r), and time (t)?
d = rt
r = d/t
t = d/r`
It is important to be flexible with all three of these formulas.
What is the area of a circle with radius r?
A = pi*r2
What is the circumference of a circle with radius r?
C = 2(pi)*r
What is the area of a square with side length x?
x2
What is the area of a rectangle with sides b and h?
A = b*h
What is the perimeter of a rectangle with sides b and h?
P = 2*b + 2*h
What is the area of a parallelogram?
The area of a parallelogram the length of one of the sides, referred to as the base times the distance between that side and the side opposite call the height. Note that the height is perpendicular to both sides.
How do you convert a repeating decimal to a fraction?
For how many places after the decimals that are repeated you put that many 9’s under the number (not as a decimal) that is repeated and then simplify. Here are some basic examples:
What are the three ways that distance, rate and time are related?
If we let d = distance, r = rate, and t = time then the formula can be expressed to equal each of them as follows.
Evaluate 2!
2! = 2*1 = 2
Evaluate 4!
4! = 4*3*2*1 = 24
Evaluate 6!
720
