Lecture 1: Intro to DFT Flashcards
(16 cards)
1
Q
- When a system is an … of observable A (when ψ is an eigenfunction of operator Â) then the expectation value of A is an … of ψ
- Âψ(r) = aψ(r)
A
- When a system is an eigenstate of observable A (when ψ is an eigenfunction of operator Â) then the expectation value of A is an eigenvalue of ψ
- Âψ(r) = aψ(r)
2
Q
- The electronic Schrodinger equation is Ĥeψ = Eeψ, which is a result of what approximation of the Hamiltonian?
A
Internuclear term (Vnn) removed via Born Oppenheimer approximation which assumed this value is fixed as nuclei are very slows with respect to electrons

3
Q
- How is the ESE approximated further?
A
- ESE still too complex to solve e.g. due to 2nd differential in KE term
- Separate into a universal (Fe) and an external potential (Vext)

4
Q
- A function is the mapping from a … to a number e.g. f(x) = y
- A functional is a mapping from a … to a number e.g. the area A under the function f(x) is a single … dependent on the whole … .
- The total energy is a functional of the … … (… – functional)
- ESE takes us from … which is known, to expectation value through …
A
- A function is the mapping from a number to a number e.g. f(x) = y
- A functional is a mapping from a function to a number e.g. the area A under the function f(x) is a single number dependent on the whole function.
- The total energy is a functional of the wave function (ψ – functional)
- ESE takes us from Vext which is known, to expectation value through ψ

5
Q
- (IMP) Outline briefly how the ESE is solved ab-intio via wavefunction theory
- (DFT is also ab initio just different appraoch)
A
- Exact ESE is solved through approximation of the ψ through variational or perturbation theory
- Uses HF of non-interacting electrons in a mean field
- Electron correlation captured through post HF methods
- E.g. CI, MP2 only differing in how they approximate ψ
6
Q
- (IMP) Why might it be more appropriate to use electron density, ρ(r) to solve the ESE
A
- Ψ depends on 3n coordinates for n electrons
- Storing this info for >100 electrons is unfeasible
- ρ(r) depends only on 3 coordinate (x,y,z), describing the probability distribution of electrons in space at that point
- much simpler as only depends on position you measure it.
7
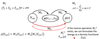
Q
- Hohenberg-Hohn (HK) theorem proves that there is a one-to-one invertible mapping between the … potential, … and the electron …, …
- This means the energy can formulated as an … density …
A
- Hohenberg-Hohn (HK) theorem proves that there is a one-to-one invertible mapping between the external potential Vext and the electron density ρ
- This means the energy can formulated as an electron density functional
8
Q
Through HK theory, how can we now approximate our Energy operator? (dntk)
A
- Energy can be expressed as a density functional where KE/Vee is a universal functional F[ρ], independent of the external potential and atomic positions (also determined by electron density and dictate energy)
- Energy as a functional of electron density is minimised through variational
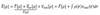
9
Q
- What is the problem with expressing the universal function F in terms of density?
A
- Expansion of the original KE term contains a 2nd derivative of ψ which cannot be formulated as a simple function of ρ
- We know that F[ρ] must exist but can’t write it down.
10
Q
- Every external potential can have only … density
- But the same density can connect to … … external potentials
- Therefore, we can calculate the GS density of …-… e-s (via Hartree theory) in an … … vs that is known
- Use this … … potentials equivalent … to calculate the energy of the system described by …
A
- Every external potential can have only one density
- But the same density can connect to two different external potentials
- Therefore, we can calculate the GS density of non-interacting e-s (via Hartree theory) in an effective potential vs that is known
- Use this made up potentials equivalent ρ to calculate the energy of the system described by vext
11
Q
- (IMP) Describe the details of this figure
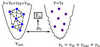
A
- Adiabatic connection of an artificial auxiliary system, vs and a real many-body system, vext connected by the same electron density, ρ
- Real system defined by coulomb interaction of all particles (complex)
- Mapped into a non-interacting system encoded by overall potential describing indirect interaction between atoms.
12
Q
- Write the energy as a functional of electron density in terms of this new auxiliary potential (dntk)
A
- The kinetic energy is now described as a functional of some artificial wavefunctions

13
Q
Where is the exchange correlation functional, EXC[ρ] derived from?
A
- The scaling parameter λ describing difference in the adiabatic connection between the artificial KE and true KE as well as the correlation and exchange energy of the non-interacting system.

14
Q
- What is our KS potential, vs made up of
A
- vs = vH + vext + vxc
- vH = Hartree potential
- vext = external potential
- vXC = exchange-correlation
–> the last describes the interaction of the electrons in our non interacting system
15
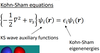
Q
- Describe the Kohn-Sham equations that form (dntk)
A
- Set of 1-particle equations form, each desrbing KE/vs of that particle
- Iteratively change {ψi} and vs until they are consistent.
- KS eigen-energies reminiscent of MOs but for effective non interacting auxiliary states
16
Q
(IMP) Describe the key differences between Wave function and KS theory
A
- Wave function theory
- Complexity in high dimensional ψ via exact ESE
- Finite sum over slater determinants
- Finite approximation of ψ àMP2,CCSD etc
- Very slow convergence to get exact Ecorr but results in exact path via systematic improvements through variational theory
- Very computationally expensive (limited to ~30 atoms)
- DFT
- Complexity in vXC (less as based on density alone)
- FInite sum over KS equations describing orbital like states
- Non-local potential in space (and time) connects all possible interactions
- Local approximations to vXC makes systematic path to true answer difficult
- Good error calculations
- Computationally very efficient