Heapsort, Priority Queues and Selection

Question 1

What is a heap?

Answer 1

A (maximum) heap is a complete binary tree having a key associated with each node, the key of each parent node being greater than or equal to the keys of its child nodes

Question 2

What two operations does the heap ADT support?

Answer 2

insert new element and delete/retrieve maximum element

These both can be performed in O(log n) time.

Question 3

What is the most common way to represent a heap?

Answer 3

In an array

Question 4

Inserting a node into heap example

Answer 4

Question 5

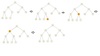
Deleting maximum node in a heap example

Answer 5

Question 6

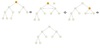
What is a priority queue?

Answer 6

A priority queue is a container for a totally-ordered set of elements (ADT)

Question 7

What operations does a priority queue support?

Answer 7

insert, peek front, delete front, decrease key (i.e. priority of an element)

Question 8

How is priority queue often implemented

Answer 8

Often is implemented using a binary heap data structure

Question 9

What can priority queues be used to represent?

Answer 9

Particular kinds of stacks and queues.

Question 10

The Selection Problem

Answer 10

• We want to find the k-th smallest item (rank k) of an unsorted collection of n elements.
• Can solve by sorting the list then pick the k-th element.

(not very efficient O(n lg n) )

• Using a binary heap we have a Θ(n + k lg n) algorithm.
• There is a Θ(n) algorithm for all input (worst case).
• There is a (simple and practical) known average-case Θ(n) algorithm, derived from quicksort, called quickselect.
• The idea is to do quicksort but only recurse into one of the two partitions that contains the k-th smallest element.

Question 11

How do you create a selection algorithm that runs in Θ(n) for all input?

Answer 11

ensure that “good” pivots are found

median-of-medians linear-time algorithm

• The divide-and-conquer recursive M.-M. algorithm:

1. 1 Partition input of n items into groups of five items.
2. Find exact median of each of the 5-element groups.
3. Find the median of these dn/5e medians (by recursion) as selected pivot.