Graphs (oh god why) Flashcards
What is a digraph?
A digraph G = (V, E) is a finite nonempty set V of nodes together with a (possibly empty) set E of ordered pairs of nodes of G called arcs

What is a graph?
A graph G = (V, E) is a finite nonempty set V of vertices together with a (possibly empty) set E of unordered pairs of vertices of G called edges
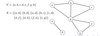
Let G = (V, E) be a digraph
If (u, v) ∈ E what can we say with respect to adjacency, outer/inner neighbours?
v is adjacent to u
v is an out-neighbor of u
u is an in-neighbor of v
Let G = (V, E) be a digraph
what is the order?
what is the size?
order: | V |, the number of nodes (often denoted by variable n)
size: | E |, the number of arcs. (often denoted by variable m or e)
Let G = (V, E) be a digraph
what is the out-degree of a node, v? If it is 0 what do we call this?
what is the in-degree of a node, v? If it is 0 what do we call this?
The out-degree of a node v is the number of arcs leaving v
The in-degree of v is the number of arcs entering v
A node of in-degree 0 is called a source and a node of out-degree 0 is called a sink
What is a walk, length of a walk, path and a cycle?
A walk in a digraph G is a sequence of nodes v0 v1 . . . vn such that, for each i with 0 ≤ i < n, (vi , vi+1) is an arc in G
The length of the walk v0 v1 . . . vn is the number n (that is, the number of arcs involved)
A path is a walk in which no node is repeated
A cycle is a walk in which v0 = vn and no other nodes are repeated
note:
A cycle in a graph is of length at least 3.
If there is a walk from u to v, then there is at least one path from u to v
Walks, paths and cycles in digraphs example
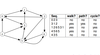
Walks, paths and cycles in graphs example
Note: e g e is not a cycle because it has only 2 arcs (e,g) and (g,e)
and by convention is said a cycle must have at least 3 arcs
The distance from u to v in G (digraph), denoted by d(u, v), is…?
the minimum length of a path from u to v.
If no path exists, the distance is undefined (or + ∞, positive infinity)
(For graphs, we have d(u, v) = d(v, u) for all vertices u and v)
What is the diameter of a digraph?
What is the relation of the radius of a digraph?
maximum distance between any two vertices
diameter: maxu,v∈V [d(u, v)]
radius: minu∈Vmaxv∈V [d(u, v)].
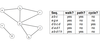
Examples of path distances in digraphs
Examples of path distances in graphs

What is the underlying graph of a digraph G = (V, E)?
G’ = (V, E’ ) where E’ = {{u, v} | (u, v) ∈ E}.
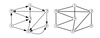
essentially a digraph with unidirectional lines replaced with bidirectional lines
What is a subdigraph of a digraph G = (V, E)?
is a digraph G’ = (V’ , E’ ) where V’ ⊆ V and E’ ⊆ E.
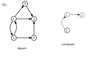
What is a spanning subdigraph?
Is one with V’ = V; that is, it contains all nodes

What is a subdigraph induced?
a subset V’ of V is the digraph G’ = (V’ , E’ ) where E’ = {(u, v) ∈ E | u ∈ V’ and v ∈ V’}
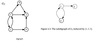
Let G be a digraph of order n.
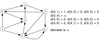
What is an adjacency matrix?
Adjacency matrix of G is the n × n boolean matrix (often encoded with 0’s and 1’s) such that entry (i, j) is true if and only if there is an arc from the node i to node j.
In the example below the first row is formed by:
does 0 travel to 0? false so 0 is put into matrix at row 0 column 0
does 0 travel to 1? true so 1 is put into matrix at row 0 column 1
does 0 travel to 2? false so 0 is put into matrix at row 0 column 2
does 0 travel to 3? true so 1 is put into matrix at row 0 column 3
and so on…
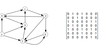
For a digraph G of order n
what is an adjacency list?
An adjacency lists representation is a sequence of n sequences, L0, . . . , Ln−1. Sequence Li contains all nodes of G that are adjacent to node i.
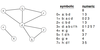
- In the example below everything under numeric heading is the adjacency list.*
- The first entry is the number of nodes.*
- Entries after that can be obtained by checking what nodes travel to which*
- for example node a travels to b and d and we have set nodes a, b, c … to be 0, 1 , 2… respectively.*
- we can insert 1 corresponding to b and 3 corresponding to d into the first row of the adjacency list.*
Digraph operations in terms of data structures
(self explanatory)

Comparative performance of adjacency lists and matrices
note: d denotes size of the adjacency list for vertex i.

Illustrating the general traversal algorithm

What is a search forest?
There may remain unvisited nodes in the digraph. In this case, we may choose another white node as root and continue. Eventually, we obtain a set of disjoint trees spanning the digraph, which we call the search forest
Suppose we have performed a traversal of a digraph G, resulting in a search forest F. Let (u, v) ∈ E(G) be an arc
When is an arc called a tree arc?
If it is not a tree arc what are the 3 other possibilities?
if it belongs to one of the trees of F
- a forward arc if u is an ancestor of v in F
- a back arc if u is a descendant of v in F
- a cross arc if neither u nor v is an ancestor of the other in F
Facts about traversal trees
Suppose we run algorithm traverse on G, resulting in a search forest F.
Let v, w ∈ V(G).
1 Let T1 and T2 be different trees in F and suppose that T1 was explored before T2. Then there are no arcs from T1 to T2.
2 Suppose that G is a graph. Then there can be no edges joining different trees of F.
3 Suppose that v is visited before w and w is reachable from v in G. Then v and w belong to the same tree of F.
4 Suppose that v and w belong to the same tree T in F. Then any path from v to w in G must have all nodes in T .
Run-time analysis of traverse
In the while-loop of subroutine visit let:
- a and A be lower and upper bounds on the time to choose a grey node.
- b and B be lower and upper bounds on the time to choose a white node.
The running time of traverse is:
- O(An + Bm) and Ω(an + bm) if adjacency lists are used, and
- O(An + Bn2 ) and Ω(an + bn2 ) if adjacency matrices are used
A DFS example

Basic properties of depth-first search
Each call to dfs_visit(v) terminates only when all nodes reachable from v via a path of white nodes have been seen.
Suppose that (v, w) is an arc. Cases:
- tree or forward arc: seen[v] < seen[w] < done[w] < done[v];
- back arc: seen[w] < seen[v] < done[v] < done[w];
- cross arc: seen[w] < done[w] < seen[v] < done[v].
Hence on a graph, there are no cross edges.
Using DFS to determine ancestors of a tree
If v is an ancestor of w in F, then seen[v] < seen[w] < done[w] < done[v] .
If v is not an ancestor of w in F, then seen[v] < done[v] < seen[w] < done[w]
A BFS example

How does DFS allow us to give a so-called pre-order and post-order labeling to a digraph?
The pre-order label indicates the order in which the nodes were turned grey.
The post-order label indicates the order in which the nodes were turned black.
Suppose that there is a cycle in G and let v be the node in the cycle visited first by DFS. If (u, v) is an arc in the cycle then it must be a…?
back arc
a digraph is acyclic iff there are no…?
back arcs from DFS
An acyclic digraph is called…?
directed acyclic graph (DAG)
An acyclic graph is a…?
forest
Arithmetic expression digraphs example

What is topological sorting?
What is its main applications?
- To place nodes of a digraph on a line so all arcs go in one direction.
Possible if and only if digraph is a DAG
- Main application:
scheduling events (arithmetic expressions, university prerequisites, etc)
Topological sorting via DFS

A graph G is connected if…?
for each pair of vertices u, v ∈ V(G), there is a path between them
A graph G is disconnected if…?
it is not connected and the maximum induced connected subgraphs are call the components of G
Nice DFS application: strong components
Nodes v and w are mutually reachable if there is a path from v to w and a path from w to v. The nodes of a digraph divide up into disjoint subsets of mutually reachable nodes, which induce strong components.
(Strong) components are precisely the equivalence classes under the mutual reachability relation.
A digraph is strongly connected if it has only one strong component.
Components of a graph are found easily by BFS or DFS. However, this doesn’t work well for digraphs (a digraph may have a connected underlying graph yet not be strongly connected). A new idea is needed.

What is the girth of a graph?
the length of the shortest cycle is called the girth of the graph.
If the graph has no cycles then the girth is undefined but may be viewed as +∞
Fact:
For a digraph we use the term girth for its underlying graph and the (maybe non-standard) term directed girth for the length of the smallest directed cycle
memes
Computing girth of a graph
- If vertex v is on at least one cycle then BFS starting at v will find it.
- On detection of a cross arc between descendants u and w, determine whether u and w are in different subtrees.
- If yes, then a cycle of length d[u] + d[w] + 1 is found.
- If no, then a cycle of shorter length is found (but avoids v).
- If d[u] = d[w] then odd length, where v common ancestor.
- Otherwise, WLOG, d[u] + 1 = d[w] and even length.
- To compute girth, we run the above procedure once for each v ∈ V(G) and take minimum.
k-colorable graphs
Let k be a positive integer. A graph G has a k-coloring if V(G) can be partitioned into k nonempty disjoint subsets such that each edge of G joins two vertices in different subsets (colors)
Bipartite graphs (digraphs)
A graph G is bipartite if V(G) can be partitioned into two nonempty disjoint subsets V0, V1 such that each edge of G has one endpoint in V0 and one in V1.
[Similar for digraphs.]


