HBX- BA - 2 Flashcards
Samples vs. Populations (and their symbols)
- Sample- A group of observations selected from a population. We generally compute statistics based on a random sample to help us estimate the parameters of a population.
- Population- The complete set of individuals or items in which an analyst or researcher is interested. When it is difficult to learn about every member of a population, random samples are often drawn from a population and analyzed in order to draw inferences about the population.
When we take a sample, we need to have a very clear understanding of the problem that we need to address. Based on that understanding, we need to do 2 things:
- What is the target population?
- What question do we want to ask?
Ex: Who will attend a conference that we are planning? Don’t ask the people planning the conference if they are going! Select 100 people at random! THEN see. Their answer is relative to the large group of people in attendance
What are parameters and statistics?
The numerical properties of a population are called parameters and those of a sample are called statistics.
A statistic is an estimate of a true value of a parameter. If a sample is sufficiently large and is representative of the population, the sample statistics should be reasonably good estimates of the population parameters.
How to enter random numbers in excel…
=RAND() to generate a random ID number between 0 and 1
- Copy and past this in other cells (or drag)
- Then you can sort them if you choose! in numerical order
DATA -> SORT ASCENDING
Suppose a college has asked you to conduct a survey to determine the percentage of 8:00 AM classrooms that were full on a given morning. The college has three classroom buildings, each containing two lecture halls. Each lecture hall has a capacity of 100 students. You randomly choose one of three buildings, and stand outside the entrance when classes let out. You ask the first 60 students leaving the building how full their class was. However, you soon realize that this sample is not random because you only went to only one of the buildings and the classes at that building may not be representative of all 8:00 AM classes. Moreover, since the students you surveyed were the first to exit the building, it’s also quite possible that they all came from the same class!
Realizing that your survey approach would not produce a random and representative sample, you gather some friends to help sample. You place one surveyor outside each building. You each randomly select 20 students leaving the buildings that morning and tally the results: 5 people decline to participate, 35 tell you that their class was full, and 20 tell you that their class was not full. Is your sample now representative of all classes that morning?
No
This question is a bit tricky. This sample still may not be representative of all classes because there is a bias in the approach. When you sample students leaving each of the buildings, you will, on average, select more people from full classes, simply because there were more people in those classes. Imagine that of the 6 classes that took place that morning, 4 were full (each having 100 students) and 2 had only 40 students each. In this case, most of the students, 400 of the total 480, were in full classes. Your sample would include more students from the full classes and therefore is not representative of all classes that took place that morning.
In addition to deciding how to select a random sample, we also must determine how large the sample should be. The appropriate sample size depends on how accurate we want our estimates of the population parameters to be. Suppose we want to sample from two populations—the first population comprises 5,000 observations and the second population comprises 5 million. If we take a sample of size 1,000 from the first population, how many times larger does the sample need to be from the second population to ensure the same level of accuracy?
No larger
We might expect that for a larger population, a larger sample size is needed to achieve a given level of accuracy, but this is not necessarily true. A sample of 1,000 is often a satisfactory representation of a population numbering in the millions, as long as the sample is randomly selected and representative of the entire population.
How big does a sample need to be to be accurate?
Sample size does not necessarily depend on population size. The right sample size depends on desired accuracy and in some cases, the likelihood of the phenomenon we wish to observe or measure.
The graphic below suggests the general relationship between accuracy and sample size. Later in this module, we will learn how to calculate the minimum required sample size to ensure a specified level of accuracy.
Although we don’t necessarily have to increase the sample size for larger populations, we may need a larger sample size when we are trying to detect something very rare. For example, if we are trying to estimate the incidence of a rare disease, we may need a larger sample simply to ensure that some people afflicted with the disease are included in the sample.
What happens to the sample mean and standard deviation as you increase the sample size?
- The sample mean and standard deviation remain the same
- The sample mean and standard deviation generally become closer to the population mean and standard deviation
- The sample mean and standard deviation generally move further from the population mean and standard deviation
- The sample mean and standard deviation vary, but do not follow a consistent pattern
The sample mean and standard deviation generally become closer to the population mean and standard deviation
- As we increase the sample size, the sample includes more members of the population, so it is less likely to include only unusual values. Therefore, as the sample grows, the sample mean and standard deviation approach the population mean and standard deviation.
What are the steps to make sure that you avoid bias in samples/surveys?
- phrasing questions neutrally- welfare vs. poor
- ensuring that the sampling method is appropriate for the demographic of the target population; choose members randomly
- pursuing high response rates. It is often better to have a smaller sample with a high response rate than a larger sample with a low response rate.
- Surveyors wish to get as high a response rate as possible. Low response rates can introduce bias if the* non-respondent’s answers would have differed from those who responded—that is, if the non-respondents and the respondents represent different segments of the population. If we do not represent a segment of the population, then our sample is not representative of the population. If resources are limited, _it is often better to take a small sample and relentlessly pursue a high response rate than to take a larger sample and settle for a low response rate_. If we have a low response rate, we should contact non-respondents and try to either increase the response rate or demonstrate that the non-respondents’ answers do not differ from the respondents’ answers.
How to make sure that you can make sound inferences from your samples:
- Make sure the sample is representative of the population by choosing members randomly to ensure that each member of the population is equally likely to be included in the sample.
- Choose the right sample size: Sample size does not necessarily depend on population size. The right sample size depends on desired accuracy and in some cases, the likelihood of the phenomenon we wish to observe or measure.
- Avoid biased results by
- phrasing questions neutrally;
- ensuring that the sampling method is appropriate for the demographic of the target population; and
- pursuing high response rates. It is often better to have a smaller sample with a high response rate than a larger sample with a low response rate.
- If a sample is sufficiently large and representative of the population, the sample statistics, x¯ and s, should be reasonably good estimates of the population parameters, μ and σ, respectively.
Sample mean
Just a single point (a point estimate). The sample mean does NOT give us an accurate representation of the true population mean.
However we can use the normal distribution to help us create a range around the sample mean that is very likely to contain the true population mean. The properties of the normal distribution help us determine how confident that we can be in our estimate.
Horizontal Axis= the VARIABLE that we are studying.
Vertical Axis= the LIKELIHOOD the different values of that variable will occur.
Formal definition: The mean, or average, value of a variable in a sample. The sample mean is denoted by x-bar. For a given sample, the sample mean is the best estimate of the true population mean, provided that the sample is randomly selected. The sample mean varies for different samples drawn from a population. For a given population, the accuracy of a sample mean generally increases as the sample size increases. In general, the lower the variability in a population, the more accurate the sample mean is as an estimate of the population mean.
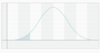
Normal distribution
The normal distribution is a symmetric, bell-shaped continuous distribution, with a peak at the mean. The mean, median and mode of a normal distribution are equal.
- How wide or narrow the curve is depends on the standard deviation. (see above)
- The location & width are completely specified by 2 parameters
- Mean
- Standard deviation
- About 68% of the probability is contained in the range reaching one standard deviation away from the mean on either side:
- *P ( μ − σ ≤ x ≤ μ + σ ) ≈ 68%**
- About 95% of the probability is contained in the range reaching two standard deviations (1.96 to be exact- which is the # we’ll use in excel for calculations) away from the mean on either side:
- *P ( μ − 2σ ≤ x ≤ μ + 2σ ) ≈ 95%**
- About 99.7% of the probability is contained in the range reaching three standard deviations away from the mean on either side:
- *P ( μ − 3σ ≤ x ≤ μ + 3σ ) ≈ 99.7%**
The amazing thing about normal distributions is that these rules of thumb hold for any normal distribution, no matter what its mean and standard deviation are. Because the normal distribution is a continuous probability distribution, the probability of the normal distribution equaling any particular value is zero (this is why we only assess the probability of a range for a continuous distribution). Because of this, we can use the terms “less than” and “less than or equal to” interchangeably when calculating probabilities for continuous distributions. Likewise we can use the terms “greater than” and “greater than or equal to” interchangeably. For example, because we know that the probability of the normal distribution equaling its mean exactly is zero, P(x=μ)=0, we can say 50% of the probability is less than the mean or 50% of the probability is less than or equal to mean: P(x
*
The standard normal curve
The standard normal curve is a normal distribution whose mean is equal to zero (μ=0), and whose standard deviation is equal to one (σ=1).
Notice that in the graph above we have labeled the x-axis twice—the upper scale shows which values are one standard deviation above or below the mean, which values are two standard deviations above or below the mean, and so on. The lower scale references those same locations on the standard normal curve, which is often easier to work with. These standardized values are known as z-values.
Cumulative Probability
- The probability of all values less than or equal to a particular value is called a cumulative probability.
- Note that cumulative probabilities are conceptually related to the percentiles of a distribution. For example, the value associated with a cumulative probability of 90% is the 90th percentile of the distribution.
To find a cumulative probability, the probability of being less than a specified value on a normal curve, we use:
Excel’s NORM.DIST function
=NORM.DIST(x, mean, standard_dev, cumulative)
- x is the value at which you want to evaluate the distribution function.
- mean is the mean of the distribution.
- standard_dev is the standard deviation of the distribution.
- cumulative is an argument that specifies the type of probability we wish to calculate. We insert “TRUE” to indicate that we wish to find the cumulative probability, that is, the probability of being less than or equal to the x-value. (Inserting the value “FALSE” provides the height of the normal distribution at the value x, which we will not cover in this course.)
For a standard normal curve, we know the mean is 0 and the standard deviation is 1, so we could find a cumulative probability using =NORM.DIST(x,0,1,TRUE). Alternatively, we use:
Excel’s NORM.S.DIST function
=NORM.S.DIST(z, cumulative)
- The “S” in this function indicates it applies to a standard normal curve.
- z is the value (the z-value) at which we want to evaluate the standard normal distribution function.
- cumulative is an argument that specifies the type of probability we wish to calculate. We will insert “TRUE”.
YOU CAN ALSO TAKE THE NORMAL DISTRIBUTION AND SUBTRACT IT FROM ONE (TO NOT DO THE CUMULATIVE)
Z-Vaule
The z-value of a data point is the distance in standard deviations from the data point to the mean. Negative z-values correspond to data points less than the mean; positive z-values correspond to data points greater than the mean.
How to find the z- value in Excel
=STANDARDIZE(x, mean, standard_dev)
- x is the value to be standardized.
- mean is the mean of the distribution.
- standard_dev is the standard deviation of the distribution.
- After standardizing, we can insert the resulting z-value into the NORM.S.DIST function to find the cumulative probability of that z-value.
What probability falls within one standard deviation of the mean?
Approximately 68%
- The phrase “within one standard deviation of the mean” means “between one standard deviation below the mean and one standard deviation above the mean.” This answer can be found using the rules of thumb for the normal distribution or by using the previous interactive. 68% of the probability lies within one standard deviation of the mean.
What is the probability of obtaining a value less than or equal to two standard deviations below the mean?
Approximately 2%
- You can use the interactive to solve this problem. If you position the slider so that it highlights the range from the far left side to “z=−2z=−2”, you can see that the area under the curve over than range is approximately 2%. This is the cumulative probability associated with z=−2z=−2. Therefore, the probability of obtaining a value less than or equal to two standard deviations below the mean is approximately 2%.
If the average height of all women is 63.5 inches and the standard deviation is 2.5 inches, approximately what percentage of women are between 58.5 and 68.5 inches tall?
95%
- 58.5 and 68.5 inches are two standard deviations from the mean, that is 63.5±2(2.5). According to the rules of thumb, approximately 95% of women’s heights fall within two standard deviations of the mean.
Recall that the z-value associated with a value measures the number of standard deviations the value is from the mean. Given that the average height of all women is 63.5 inches and the standard deviation is 2.5 inches, what z-value corresponds to 61 inches?
Suppose we want to know the percentage of women who are shorter than 63 inches. Since the mean is 63.5 inches, we can estimate that less than 50% are shorter than 63 inches. How do we calculate the exact percentage What excel function can we use to help us solve this?
To find a cumulative probability, the probability of being less than a specified value on a normal curve, we use:
Excel’s NORM.DIST function
=NORM.DIST(x, mean, standard_dev, cumulative)
- x is the value at which you want to evaluate the distribution function.
- mean is the mean of the distribution.
- standard_dev is the standard deviation of the distribution.
- cumulative is an argument that specifies the type of probability we wish to calculate. We insert “TRUE” to indicate that we wish to find the cumulative probability, that is, the probability of being less than or equal to the x-value. (Inserting the value “FALSE” provides the height of the normal distribution at the value x, which we will not cover in this course.)
For a standard normal curve, we know the mean is 0 and the standard deviation is 1, so we could find a cumulative probability using =NORM.DIST(x,0,1,TRUE). Alternatively, we use:
Excel’s NORM.S.DIST function
=NORM.S.DIST(z, cumulative)
- The “S” in this function indicates it applies to a standard normal curve.
- z is the value (the z-value) at which we want to evaluate the standard normal distribution function.
- cumulative is an argument that specifies the type of probability we wish to calculate. We will insert “TRUE”.
How to find the z- value in Excel
=STANDARDIZE(x, mean, standard_dev)
- x is the value to be standardized.
- mean is the mean of the distribution.
- standard_dev is the standard deviation of the distribution.
- After standardizing, we can insert the resulting z-value into the NORM.S.DIST function to find the cumulative probability of that z-value.
58%
- Since 42% of women are shorter than 63 inches, the percentage of women that have heights greater than or equal to 63 inches is 1–0.42 =0.58, or 58%. We could also calculate this directly using the Excel function 1–NORM.DIST(63,63.5,2.5,TRUE)=0.58, or 58%.
Suppose we want to find the value associated with the cumulative probability 99% for the distribution of women’s heights. In other words we might want to know the 99th percentile of women’s heights.
=NORM.INV(probability, mean, standard_dev)
- probability is the cumulative probability for which we want to know the corresponding x-value on a normal distribution.
- mean is the mean of the distribution.
- standard_dev is the standard deviation of the distribution.
Alternatively, we could use the Excel function NORM.S.INV. The “S” in this function indicates that it applies to a standard normal curve. Since we are working with the standard normal curve, we can interpret the resulting value as a z-value.
=NORM.S.INV(probability)
- probability is the cumulative probability for which we want to know the corresponding x-value on a standard normal distribution.
For example, if we wanted to know the z-value for the 95th percentile on a standard normal curve, we would enter =NORM.S.INV(0.95)=1.645. Equivalently, we could enter =NORM.INV(0.95,0,1)=1.645.
Suppose we want to calculate the value associated with the upper tail of a distribution, that is, the probability of an outcome greater than a specified value. We first need to calculate the value associated with the corresponding cumulative probability, which is one minus the probability of the upper tail. For example, the height that 1% of women are taller than is the same as the height that 99% of women are shorter than.
Thus we calculate the value associated with the top 1% by entering the function =NORM.INV(0.99,63.5,2.5)≈69.
Suppose we want to calculate the value associated with the upper tail of a distribution, that is, the probability of an outcome greater than a specified value. How is this done?
We first need to calculate the value associated with the corresponding cumulative probability, which is:
1 - minus the probability of the upper tail
For example, the height that 1% of women are taller than is the same as the height that 99% of women are shorter than. Thus we calculate the value associated with the top 1% by entering the function =NORM.INV(0.99,63.5,2.5)≈69.
What if we want to find a range of values associated with a probability that is not a cumulative probability? For example, suppose we want to know the range of values associated with the “middle” 99% of a normal distribution?
The normal curve is symmetrical, so we know that the middle 99% of the distribution comprises 49.5% on either side of the mean and excludes 0.5% on each of the tails. Thus we can find the value corresponding to the left side of the range using the NORM.INV function evaluated at 0.5% and the right side using the NORM.INV function evaluated at 99.5%.
In this case, the values associated with the middle 99% are NORM.INV(0.005,63.5,2.5)=57.1 and NORM.INV(0.995,63.5,2.5)=69.9.
Central Limit Theorem
A theorem stating that if we take sufficiently large randomly-selected samples from a population, the means of these samples will be normally distributed regardless of the shape of the underlying population. (Technically, the underlying population must have a finite variance.)
How this works…..
- Take a random sample from a population
- That sample has a mean- plot it on a graph!
- Then take another sample- this sample ALSO has a mean (put IT on the graph)
- If we did this TONS of times- it would form a normal distribution!
No one actually does this…. In the REAL world we take ONE sample!
This allows us to ignore the underlying distribution of the population that we want to learn about. We now know that the mean of a sample is PART of a normal distribution. Specifically- we know that the sample mean falls somewhere in a normal distribution that is centered at the true population mean. Because of this we can disregard the underlying distribution of the population and only focus on the sample.
According to the Central Limit Theorem, if we take large enough samples, the distribution of sample means will be normally distributed regardless of the shape of the underlying population. This population distribution will result in a normally distributed distribution of sample means. Note that there are other correct answers.
What is the standard deviation of the distribution of sample means?
Define Confidence intervals (for a population mean) and list the confidence interval equation.
A range constructed around a sample mean that estimates the true population mean. The confidence level of a confidence interval indicates how confident we are that the range contains the true population mean. For example, we are 95% confident that a 95% confidence interval contains the true population mean. The confidence level is equal to 1 – significance level.
What are the equations for deviations 1, 2, & 3 standard deviations away from the mean (on both sides)? Also, what are the numbers associated with these (that we used in equations)?
-
68% Confidence Interval = 1
1 Standard Deviation away from the mean (on both sides)
(1 is what “z” equals in equations when you want to use this confidence interval???) -
95% Confidence Interval = 1.96
2 Standard Deviations away from the mean (on both sides)
(1.96 is what “z” equals in equations when you want to use this confidence interval???) -
99.7% Confidence Interval = 3
3 Standard Deviations away from the mean (on both sides)
(3 is what “z” equals in equations when you want to use this confidence interval???)
The standard deviation of the distribution of sample means is _______ of that of the population distribution.
The standard deviation of the distribution of sample means is DIFFERENT of that of the population distribution.
For the distribution of sample means:
2 Standard Deviations = 2 times (population mean / square root of sample size)
What does it mean to say that 95% of samples will have confidence intervals that contain the true population mean.
We are not saying that 95% of the time our sample mean IS the population mean. What we’re saying is that for 95% of all random samples -a range that is 2 standard deviations wide and is centered at the sample mean contains the population mean.
Another way to explain it: if we took 20 samples from a population and then draw a confidence interval around each samples mean. On average, 95% of these would actually contain the true population mean. (19 out of 20)
Which of the following would increase the width of the confidence interval? Select all that apply.
- Increasing the sample mean
- Increasing the confidence level
- Increasing the sample size
- Decreasing the sample size.
- Increasing the sample mean
Increasing the sample mean affects where the confidence interval is centered, not how wide the interval is. Use the interactive and review the confidence interval equation to help answer this question. -
Increasing the confidence level
Increasing the confidence level means that we must be more confident that the actual populationmean lies within our range. The confidence level must be wider to increase the likelihood that it captures the true population mean. Note that confidence level determines the z-value, which in turn drives the width of the interval. Note that another option is also correct. - Increasing the sample size
Increasing the sample size will result in a more accurate prediction and, therefore, a narrower confidence interval. Use the interactive and review the confidence interval equation to help answer this question. Think about how the confidence level and the sample size affect the width of a confidence interval. Note that n is in the denominator, so as n increases, s / (square root of n) decreases, that is, the width of the confidence interval decreases. -
Decreasing the sample size
Decreasing the sample size will result in a less accurate prediction, and, therefore, a wider confidence interval. Note thatn is in the denominator, so as n decreases, s / (square root of n) increases, that is, the width of the confidence interval increases.
THE BOLD ONES ABOVE ARE THE CORRECT ONES
What’s the Confidence Interval/Margin of error Equation in Excel?
**FOR LARGE SAMPLES (30 and above)
=CONFIDENCE.NORM(alpha, standard_dev, size)**
- alpha, the significance level, equals one minus the confidence level
- (for example, a 95% confidence interval would correspond to the significance level 0.05).*
- standard_dev is the standard deviation of the population distribution. We will typically use the sample standard deviation, s, which is our best estimate of our population’s standard deviation.
- size is the sample size, n.
FOR SMALL SAMPLES (30 and below)
If we don’t know anything about the underlying population, we cannot create a confidence interval with fewer than 30 data points because the properties of the Central Limit Theorem may not hold. However, if the underlying population is roughly normally distributed, we can use a confidence interval to estimate the population mean as long as we modify our approach slightly. We can gain insight into whether a data set is approximately normally distributed by looking at the shape of a histogram of that data. There are formal tests of normality that are beyond the scope of this course.
To estimate the population mean with a small sample, we use a t-distributioninstead of a “z-distribution”, that is, a normal distribution.A t-distribution looks similar to a normal distribution but is not as tall in the center and has thicker tails. These differences reflect that fact that a t-distribution is more likely than a normal distribution to have values farther from the mean. Therefore, the normal distribution’s “rules of thumb” do not apply. The shape of a t-distribution depends on the sample size; as the sample size grows towards 30, the t-distribution becomes very similar to a normal distribution.
=CONFIDENCE.T(alpha, standard_dev, size)
- alpha, the significance level, equals one minus the confidence level
- (for example, a 95% confidence interval would correspond to the significance level 0.05).*
- standard_dev is the standard deviation of the population distribution. We will typically use the sample standard deviation, s, which is our best estimate of our population’s standard deviation.
- size is the sample size, n.
Like CONFIDENCE.NORM, CONFIDENCE.T returns the margin of error, which we can add and subtract from the sample mean.
Suppose we want to estimate the average body mass index (BMI) for adults in the United States. BMI is an indicator of body fat. We randomly sample 100 adults and calculate their BMIs based on each individual’s height and weight. We would like to be 95% confident that our estimate includes the average BMI for all U.S. adults. To do this, we will construct a 95% confidence interval around the average BMI of the sample.
What are the steps to do this? What do the lower and upper bounds of the confidence interval tell us?
-
Calculate the sample mean and standard deviation of the sample
=AVERAGE and =STDEV.S -
Calculate the confidence interval’s margin of error
=CONFIDENCE.NORM(alpha, standard_dev, size)
(.05, standard deviation, sample size) - Calculate the lower & upper bounds of the 95% confidence interval by adding and and subtracting the margin of error from the mean.
What do the lower and upper bounds of the confidence interval tell us?
MY ANSWER: We are 95% confident that the average body mass index (BMI) for all adults in the United States lies between 25.64 and 28.14. The lower and upper bounds of the confidence interval create a range that this BMI average for all adults in the US (the true population mean) will most likely lie. Also, the length from the lower bound to the upper bound is two deviations wide.
This does NOT mean that there is a 95% chance that the population mean for BMI falls in this range. Rather, it only means that we can be 95% confident that the true population mean is within this range.
Suppose we want to construct a 95% confidence interval for the true mean BMI that has a margin of error of 1 kg/m2. That is, our desired level of accuracy is 1 kg/m2; we want to be 95% confident that our sample mean is within 1 kg/m2 of the true population mean.
How large does our sample size need to be in order to produce this level of accuracy with 95% confidence?
How large must our sample size be for the 95% confidence interval to be within 1 kg/m2 of the true average BMI? Since we don’t know σ, the standard deviation of the population, let’s use the standard deviation of our previous sample (s=7.10) as an estimate.
How large must our sample be for the 68% confidence interval to be within 1 kg/m2 of the true average BMI? Since we don’t know σ, the standard deviation of the population, let’s use the standard deviation of our previous sample (s=7.10) as an estimate.
What is a Dummy Variable? And what’s the excel formula for it?
Dummy Variable
A variable that takes on one of two values: 0 or 1. Dummy variables are used to transform categorical variables into quantitative variables. A categorical variable with only two categories (e.g. “heads” or “tails”) can be transformed into a quantitative variable using a single dummy variable that takes on the value 1 when a data point falls into one category (e.g. “heads”) and 0 when a data point falls into the other category (e.g. “tails”). For categorical variables with more than two categories, multiple dummy variables are required. Specifically, the number of dummy variables must be the total number of categories minus one.
=IF(logical_test,[value_if_true],[value _if_false])
- Enter the formula above in the first cell
- Copy and paste it (or drag it) into the other cells
- To continue the process…..
- Calculate the mean of the dummy variable, which is equivalent to the sample proportion, and
- the standard deviation.
- Remember that you can use either Excel’s descriptive statistics tool or the functions AVERAGE and STDEV.S*
- calculate the confidence interval using the appropriate formula for this sample size.
How is the confidence interval for a proportion calculated?
Not sure if this is necessary to know for the test… but
How to Verify the Sample Size for Low Probability Events
Sample size is particularly important when dealing with very small (or very large) proportions.
Suppose we are sampling to find the prevalence of Amyotrophic Lateral Sclerosis (ALS), a disease commonly known as Lou Gehrig’s disease. In the United States, an estimated six to eight people per 100,000 have ALS. That is, the likelihood that a person in the U.S. has ALS is between 0.00006 and 0.00008, or between 0.006% and 0.008%. Would our sample be useful if we surveyed 100 people? No. Since the proportion we are estimating is very small, we need to have a large enough sample to make sure that it includes at least SOME people with the disease. Otherwise, we will not have enough data to obtain a good estimate of the true proportion.
The following guidelines are typically used when estimating proportions to ensure that a sample is large enough to provide a good estimate. The sample size n must be large enough to satisfy both conditions:
n= the sample size p= the mean
For a normal distribution with mean 47 and standard deviation 6, find the value associated with the top 10% of outcomes.
To solve problems like this, we can think in terms of cumulative probabilities and use the NORM.INV function. The value associated with the top 10% is the same as the value corresponding to the bottom 90%, so we need to find the value associated with a cumulative probability of 90%. Using-
NORM.INV(0.90,B1,B2)=55, we find that 90% of the distribution’s values are less than 55; thus 10% of the distribution’s values are greater than 55.
If we wish, instead of first computing 100%–10%=90%, we can embed that formula in the function using NORM.INV(1–0.10,B1,B2)=55. You must link directly to cells to obtain the correct answer.
For a normal distribution with mean 425 and standard deviation 50, find the value associated with the top 30%.
The value associated with the top 30% is the same as the value corresponding to the bottom 70%, so we need to find the value associated with a cumulative probability of 70%.
- Using NORM.INV(0.70,B1,B2)=451, we find that 70% of the distribution’s values are less than 451. Thus, 30% of the distribution’s values are greater than 451. If we wish, instead of first computing 100%–30%=70%, we can embed that formula in the function using NORM.INV(1–0.30,B1,B2)=451. You must link directly to cells to obtain the correct answer.
For a normal distribution with mean 47 and standard deviation 6, find the upper value and lower value of the range of outcomes associated with the middle 25%.
