HANDOUT 3 - Performance index and nominal/true stress

Question 1

What is the procedure to optimise performance?

Answer 1

The produce:

(1) Identify objective (what is to be maximised or minimised, e.g. mass)
(2) Identify functional constraints (e.g. specified stiffness?)
(3) Identify geometrical constraints (which dimensions are fixed, and which can vary?)
(4) Eliminate free variables, and identify performance index of properties

Question 2

A lightweight tensile tie of specified length L is required to carry a load F. The maximum allowable extension is d. The tie has a uniform prismatic crosssection, but its area A may be varied.

Using the 4 step procedure, find the perfomance index.

Answer 2

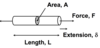
Step 1: Objective: minimum mass ⇒ m = pLA

Step 2: Functional constraint: specified stiffness = AE/L

Step 3: Geometric constraints: fixed L, free variable A Hence stiffness constraint becomes: FL/d = AE = constant

(i.e. as material is changed, area is adjusted to give required stiffness).

Step 4: Eliminate free variable A in the objective equation: Mass m = pLA = L²(F/d)(p/E) i.e mass proportional to (p/E)

Question 3

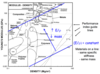
If E/p is a perfoermance index for a design find a selection of materials that are stiffer and lighter than steel: E > 210 GPa, p < 7.6 Mg/m3.

(Use the Modulus - density property chart)

Answer 3

E/p = constant, C

logE = logp + logC

Plot on graph ⇒

Selection results:

Technical ceramics

Composites

Bamboo

Question 4

What materials should generally be excluded when secondary constraints for a material is toughness?

Answer 4

• Exclude all ceramics and glass

Question 5

If a material has poor resistance to corrosion do we exclude that material (if corrosion resistance is required)? why?

Answer 5

No need to exclude material, but implies the need for protection(e.g. painting), bringing in additional costs.

Question 6

Which composites have the most manufacturing limits and why?

Answer 6

• Ceramics are limited, processed by powder compaction.
• Fibre composites: difficult to shapel must usually be joined by adhesives.
• Wood: some shape limitations, well-suited to mechanical joining and adhesives.
• metals/polymers: easy to form into wide range of shapes.

Question 7

What is the performance index for bending stiffness?

Answer 7

E^1/3/p = c

lines of slope 3 on MODULUS-DENSITY graph.

Question 8

Does knowing the numerical values for the deisgn constants help in choosing the material?

Answer 8

Loading details in bending (e.g. distributed load, cantilever etc) do not affect the outcome - only the constant in the stiffness equation.

• best materials can again be identified without numerical values for the design constants (load, deflection, length)

Question 9

What performance index does E^1/2/p indicate?

Answer 9

Performance index that arises for beams of constant shape (e.g. solid square sections), varying width and depth in proportion.

Question 10

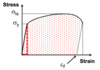
For the stress-strain graph below, show which area under the graph represents the elastic stored energy per unit volume and also the plastic work per unit volume.

Answer 10

Question 11

Define annealed

Answer 11

Softened, by heat treatment

Question 12

Define drawn

Answer 12

previously hardened, by stretching

Question 13

Equation for nominal stress, σ_n

Equation for nominal strain, ε_n

Answer 13

σ_n = -F/A_o

ε_n=(L-L_o)/L_o

Question 14

Give reasons why its often desirable to use non-destructive testing(NDT)?

Answer 14

• may need to return component to service after testing
• size/shape may not allow manufacture of tensile or compressive sample
• tensile/compression testing can be expensive and time-consuming

Question 15

Explain the vickers hardness test.

Answer 15

• a diamond pyramid is pressed into the surface under a constant load
• local plastic deformation occurs until load is supported
• load removed and the resulting indent size, d, is measured.
• A = (d/2^0.5)² = d²/2

Question 16

What is the equation that defines hardness?

Answer 16

H = Load/projected area of indent = F/A

units: usually kg/mm² can also be expressed in MPa.

Question 17

What is the relationship between hardness and yield stress (mathematically)?

Answer 17

H ≈ 3σ_y

Question 18

Define ( with no equations ) what a nominal contact area is and what a true contact area is, with diagrams?

Answer 18

The true contact area, A_t, is the sum of the area of all of the contact points where the asperities meet.

Question 19

How does the surface oxidation of metals affects the friction of the metal?

Answer 19

Most metallic surfaces carry a thin layer of oxide, due to exposure to the atmosphere. Hence the shear strength of asperity contacts is more likely to reflect the shear strength of the oxide, not the metal.

Nonetheless, the true contact area is still dependent on yielding of the metal, and both F and N still depend on A_t – so a constant friction coefficient is expected.

Question 20

Why do low modulus materials such as rubberhave high friction coefficients?

Answer 20

When rubber makes contact with a rough surface, it can deform around the asperities to give a “conforming contact” – the true area approaches the nominal area of contact.

The shear strength (due to adhesion between the materials) is lower, but this is outweighed by the much larger contact area. This is one of the reasons that rubber is so effective for providing high friction coefficients.

Question 21

How does lubrication work?

Answer 21

Lubrication works by the entrapment of a fluid (such as oil) between the surfaces, preventing solid-solid asperity contact.

The shear resistance now comes from shearing the oil – hence leading to a low friction coefficient.

Question 22

Derive the equation σ_t = σ_n(1+ε_n) knowing that:

σ_t​ = F/A

σ_n = F/A_o

Treat the sample as a constant volume: A_ol_o=Al

Answer 22

σ_t​ = σ_n(A_o/A) = σ_n(l/l_o)

nominal strain: ε_n = (l-l_o)/l_o = l/l_o - 1 ⇒ l/l_o = 1 + ε_n

Hence: σ_t = σ_n(1+ε_n)

true stress > nominal stress

True stress is easily calculated from nominal stress-strain data, but only as far as onset of necking in tension.

Question 23

Describe a way to visualise and to calculate true strain.

Answer 23

True strain is more difficult to visualise – each increment of extension dl is divided by the current length (not the initial value), to give an increment of true strain: dε=dl/l , total true strain is found by integrating between original and final lengths.

Question 24

What is the equation linking true strain to nominal strain?

Answer 24

ε_t = ln(1 + ε_n)

true strain < nominal strain (for ε_n > 0)

Question 25

When is nominal strain ≈ true strain?

Answer 25

ε_t = ln(1+ε_n) = ε_n + high order terms

so ε_t ≈ ε_n for ε_n << 1

Question 26

Draw a general stress-strain curve(that goes past yield point) for true/nominal stresses/strains.

Answer 26

Question 27

What is strength defined as?

Answer 27

nominal stress at the elastic limit