HANDOUT 2 - Component design and composites Flashcards
What is the equation for Poisson’s ratio, v?
v = - Lateral strain/Tensile strain
(note minus sign, so v is positive)
Note: Laterial strain is not due to volume conservation, but reflects the way atomic bonds deform under load.
What does Poisson’s ratio matter in design?
- not important in most deisgn with uniaxial loads(e.g truss)
- important when stress state is 2D or 3D (constrained expansion)
- important in vibration of plates ( affects frequencies of vibration modes )
- important in large strain bending, giving anticlatic curvature.
Consider a unit cube of material, under a general set of normal stresses.
Find the resulting strains.
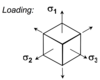
Strains due to stress σ1 :
ε1 = σ1/E
ε2 = (-vσ1)/E
ε3 = (-vσ1)/E
Repeat for each stress in turn, and sum the strains:
ε1 = (σ1 -vσ2 - vσ3)/E
ε2 = (-vσ1 σ2 - vσ3)/E
ε3 = (-vσ1 -vσ2 + σ3)/E
Give the equation for dilation, ∆
(also known as volumetric strain)
∆ = △V/Vo
Consider the unit cube, for a general strain state ( ε1 , ε2 , ε3 ):
Initial volume : Vo= 1
Find the final volume.
Final cube dimensions : (1+ε1 , 1+ε2 , 1+ε3 )
v = (1+ε1) x (1+ε2) x (1+ε3)
= 1 + ( ε1 + ε2 + ε3) + (higher order terms)
so ∆ = ε1 + ε2 + ε3
For small strains (ε <<1)
A state of hydrostatic stress is when all three normal stresses are equal, under uniform external pressure p: σ1 = σ2 = σ3 = -p
This loading occurs in ceramic manufacturing.
Calculate the strain of each axis of the cube and hence find the dilation and also the bulk modulus, K.
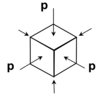
ε1 = ε2 = ε3 = (-p + vp + vp)/E = -p(1-2v)/E
Hence dilation is: ∆ = -3p(1-2v)/E
K = E/(3(1-2v))
What is the equation for bulk modulus, K?
(units: GPa)
K = Hydrostatic stress/Volumetric strain
Why is rubber incompressible? ( Don’t explain in terms of microstructure, explain in terms of posion ratio)
Rubber has a poison ratio of v = 0.5 which leads to a bulk modulus of infinity.
Define shear stress
Force per unit area carried parallel to a plan within the material.
What is the equation for the shear modulus G?
G = Shear stress/Shear strain = τ/γ (units: GPa)
Shear strain: γ = w/lo
What is the eqatuon that relates shear modulus G and Young’s modulus E?
G = E/(2(1+v))
define isotropic
same properties in all directions
Consider a cube of material fitted into a square-section slot in a rigid plate, and loaded with a compressive stress σ1.
Find the “effective modulus”. (σ1/ε1)
ε3 = 0 = -vσ1/E + σ3/E ( note σ2 = 0 )
Hence: σ3 = vσ1 (both compressed)
Strain in the 1-direction (due to both stresses) is given by:
ε1 = σ1/E - vσ3/E = σ1/E - v2σ1/E = σ1(1-v2)/E
Hence the “effective modulus”, σ1/ε1 = E/(1-v2)
What is the equation for thermal strain, εthermal?
εthermal = α x ∆T
When total strain = 0, εelastic = -εthermal
If a metal railway track experiences a thermal expansion during a hot day what can be done to its design to stop it buckling?
- Leaving expansion gaps
- Install under tension
Find the strain the top layer experiences, when a temperature drop of ∆T causes the two layers to thermally expand by different amounts.
Top layer has a thermal expansion coefficient of α1 and bottom layer has a thermal expansion coefficient of α2.
final length = that of top layer = lo(1-α2∆T)
Superpose tensile stress in surface layer, to increase its length from its contracted length, to match that of substrate:
- change in length: ∆l = loα1∆T - loα2∆T
- strain in surface layer: ∆l/(lo(1-α1∆T))
= ((α1-α2)∆T)/(1-α1∆T)
Since (α1∆T) <<1, strain = (α1 - α2)∆T
Give the different ways to measure the Youngs moldus, E, of a material and give the advantages/disadvantages for these methods.
Tensile Testing:
- elastic extensions are small hence difficult to measure precisely.
- measurement from machine must allow for flexure of machine.
Bending stiffness of a beam:
Beam of uniform cross-section loaded in 3-point bending.
- Equation can be found in structures data book.
- Bending gives more more deflection for given load than tension.
- E sensitive to L and D: requires accurate measurement of dimensions.
Natural frequency of vibration:
- Beam supported at nodal points and set vibrating.
- Measuring frequency more accurate than deflection
- Calculated E still sensitive to beam/plate dimensions.
Speed of Sound in the material:
Measure E by measuring vt:
- strike a bar of material on one end
- time the longitudinal wave reflected from far end of the bar.
- accuracy depends on precise time measurement, which is relatively easy with piezoelectric transducers.
What are the properties of amorphous metals?
- mechanically hard; magnetically - may be hard or soft
- very low damping (little energy lost in elastic collisions).
What are the two mechanisms for “alloying” polymers?
Copolymers: more than one monomer polymerised together - only a few combinations will do this.
Polymer blends: molecular-scale mixtures of two polymer chains, without cross-linking.
What is the glass transition temperature?
In polymers, the weaker secondary bonds are overcome by thermal energy at a lower temperature: the glass transition temperature, Tg.
Explain how amorphous thermoplastics behave above Tg.
Melt to a viscous liquid (entangled molecules slide over one another).
Explain how semi-crystalline thermoplastics behave above Tg.
Amorphous region melt, crystalline regions survive to higher melting point, Tm, above which a viscous liquid forms.
Explain how elastomers and thermosets behave above Tg.
Secondary bonds melt at Tg but cross-links do not - on heating the polymer does not melt, but decomposes or burns.
Give the consequences for processing and environmental impact of:
Thermoplastics
Elastomers/Thermosets
Thermoplastics:
Easy to re-mould, weld, and recycle
Viscosity falls with T: mould 150*C above Tg
Elastomers/Thermosets:
Mould once only
cannot recycle (limited re-use)
Draw the Young’s modulus vs Temperature graph for semi-crystalline thermoplastics, one with a high degree of crystallinity and one with a low degree of crystallinity.
- At high crystalline fractions, glass transition has no effect on E.
- At Tm crystalline regions melt: viscous flow.
- crystalline regions stiffer than amorphous: higher E below Tg.
Draw the Young’s modulus vs Temperature graph for thermosets( high degree of cross-linking ) and for elastomers ( low degree of cross-linking ).
- Highly cross-linked, no effect of glassy transition.
- Stiffer than thermoplastics in the glassy region; E falls slowly on heating.
What is the equation used to find out the E of a foam material?
Efoam/Esolid = (pfoam/psolid)2
Give the three main composite geometries (with diagrams).
Particulate:
metal -ceramic: Al-SiC
polymer - ceramic: “filled polymers”
Fibres:
carbon/glass/kevlar fibre - polymer
Laminates:
plywood
Give the composite processing for the three types of composites.
Particulate composites:
- Add micron-scale particles to melt before casting or moulding.
Fibre composites:
- Short chopped fibres: mix with resin, shape in a mould.
Laminates:
- wood etc: stack and glue thin layers
- long-fibre composites: stack multiple layers of prepreg with different fibre orientations.
define anisotropic
Stiffness differs parallel and perpendicular to the layers
What is the equation for longitudinal modulus ( Young’s modulus parallel to layers of a composite ) ?
Ec=σc/εc = VfEf + (1-Vf)xEm
(denoted EII in Databook)
What is the equation for the transverse modulus of a laminate composite?
Ec= (Vf/Ef + (1-Vf)/Em)-1
Are particulate composites upper bound or lower bound on the graph shown?
Are fibre composites upper bound or lower bound on the graph shown?
Particulate composites:
- isotropic ( same in all directions )
- close to lower bound (equal stress)
Fibre composties:
- anisotropic (stiffer parallel to fibres)
- parallel to fibres: upper bound exact(equal strain)
- perpendicular to fibres: close to lower bound (equal stress)
