Geometry (Problems 2.) Flashcards
Find the x value in the triangle below.

x = 13
Find the x value in the triangle below.
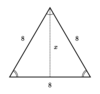
x = √48
Find the length of the unknown sides in the triangle shown below
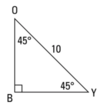
5√2
Solve for the missing sides of the triangle.
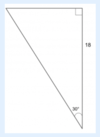
Hypotenuse = 12√3
Side B (opposite 30° angle) = 6√3
What is the Sin, Cos, and tan of angle “G.”
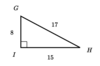
Sin (G) = 15/17
Cos (G) = 8/17
Tan (G) = 15/8
Find the missing sides of the triangle
Round your answer to the nearest hundredth.

x = 8.62
y = 2.66
Find the missing angle of the triangle
Round your answer to the nearest hundredth.
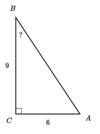
33.69º
Find the missing angle “B”.
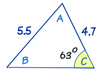
angle “B” = 49.59°
Find the missing side “AB”

side “AB” = 7.71
Find the missing angles
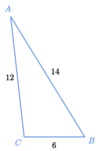
angle “A” = 25.21°
angle “B” = 58.41°
angle “C” = 96.38°
Find the missing side “BC”.

side “BC” = 14.62
In the figure below, line (AD) and line (CE) are diameters of circle P.
What is the measure of Arc (AEB) in degrees?
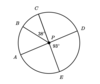
305°
In the figure below, line (BC) is a diameter of circle P. The length of line (BP) is 3 Units.
What is the length of curve (ACD)?
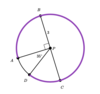
(65/12)π
or
17.02
In the figure below, the radius of circle P is 18 units. The length of Arc (BA) is 14π.
What is the measure of Arc (BC) in degrees?
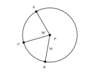
64°
Convert the angle Ø = (23π/20) radians to degrees.
207°
Convert the angle Ø = 260° to radians.
13π/9 Radians
What is the exact length of Curve (DAC) on Circle P?

5π
What is the arc measure of Curve (CD), in radians?

π/5
What is the area of the Sector?

45π/4
If angle “ABC” measures 70º, what does angle “ADC” measure?

angle “ADC” = 35°
What is the Radius of circle “O”

Radius = 6.5 Units
What is the measure of Angle “ACO” ?

Angle “ACO” = 90°
What is the measure of Angle “A” ?

Angle “A” = 88°
What is the perimeter of Quadrilateral “ABCD” ?

Quadrilateral “ABCD” = 44.4 Units
The equation of a Circle is given below
What is the Center and Radius?

Center = (-1.6 , -9.8)
Radius = 5.10 Units
A Circle has a radius of √13 and is centered at (-9.3, 4.1)
write the equation of the circle.

The equation of a Circle is given below
What is the Center and Radius?

Center = (9 , -10)
Radius = 2 Units


